题目内容
【题目】如图,在正方形ABCD中,点E、点F分别在边BC、DC上,BE=DF,∠EAF=60°.
(1)若AE=2,求EC的长;
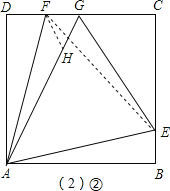
(2)若点G在DC上,且∠AGC=120°,求证:AG=EG+FG.

【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】试题分析:(1)连接EF,根据正方形的性质求出AB=AD,∠B=∠D,然后利用“边角边”证明△ABE和△ADF全等,根据全等三角形对应边相等可得AE=AF,从而得到△AEF是等边三角形,根据等边三角形的三条边都相等可得EF,再判断出△CEF是等腰直角三角形,根据等腰直角三角形的直角边与斜边的关系求解即可;
(2)在AG上截取GH=FG,可得△FGH是等边三角形,根据等边三角形的性质可得FH=FG,∠FHG=60°,再求出∠AFH=∠EFG,然后利用“边角边”证明△AFH和△EFG全等,根据全等三角形对应边相等AH=GE,然后证明即可.
试题解析:(1)解:如图,连接EF,
在正方形ABCD中,AB=AD,∠B=∠D,
在△ABE和△ADF中, 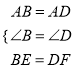 ,
,
∴△ABE≌△ADF(SAS),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形,
∴EF=AE=2,
∵BE=DF,BC=CD,
∴BC﹣BE=CD﹣DF,
即CE=CF,
∴△CEF是等腰直角三角形,
∴EC=![]() EF=
EF=![]() ×2=
×2=![]() ;
;
(2)如图(2)②在AG上截取GH=FG,
∵∠AGC=120°,
∴∠AGF=60°,
∴△FGH是等边三角形,
∴FH=FG,∠FHG=60°,
∵△AEF是等边三角形,
∴∠AFE=60°,
∴∠AFE=∠GFH=60°,
∴∠AFE﹣∠EFH=∠GFH﹣∠EFH,
即∠AFH=∠EFG,
在△AFH和△BFG中, 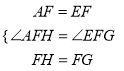 ,
,
∴△AFH≌△EFG(SAS),
∴AH=GE,
∴AG=AH+GH=EG+FG,
即AG=EG+FG.