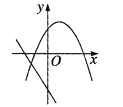题目内容
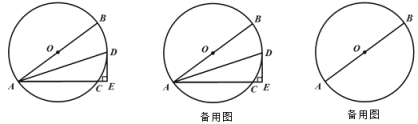
【题目】如图,在平面直角坐标系xOy中,A为x轴上一点,以OA为直径的作半圆M,点B为OA上一点,以OB为边作□OBDC交半圆M于C,D两点.
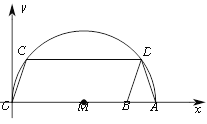
(1)连接AD,求证:DA=DB;
(2)若A点坐标为(20,0),点B的坐标是(16,0),求点C的坐标.
【答案】(1)详见解析;(2)点B的坐标是(2,6)
【解析】
(1)运用平行四边形的性质、四边形的内接圆以及等腰三角形的性质作答即可;
(2) 作DE⊥x轴于点E,延长DC交y轴于点F,连接MD,构造直角三角形,运用勾股定理解答即可.
(1)证明:∵四边形OBDC是平行四边形
∴∠C=∠OBD
∵四边形OADC内接于⊙M
∴∠C+∠A=180°
∵∠OBD+∠ABD=180°
∴∠A=∠ABD
∴DA=DB

(2)作DE⊥x轴于点E,延长DC交y轴于点F,连接MD,则AE=BE=2,
∴MD=MA=10,ME=8
在Rt△MDE中,由勾股定理可得DE=6
∵BD=OC,CF=DE=6
∴△OCF≌△DBE (HL)
∴CF=BE=2
故点B的坐标是(2,6)

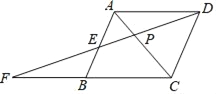
【题目】如图,在4×4的正方形网格中,△ABC和△A'B'C'的顶点都在边长为1的小正方形的格点上.

(1)填空:∠BAC= °,AB= ;
(2)判断:△ABC和△A'B'C这两个三角形相似吗?为什么?
【题目】小明利用函数与不等式的关系,对形如![]() (
(![]() 为正整数)的不等式的解法进行了探究.
为正整数)的不等式的解法进行了探究.
(1)下面是小明的探究过程,请补充完整:
①对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如表格:
的图象可以得到如表格:
|
|
|
| + | ﹣ |
由表格可知不等式![]() 的解集为
的解集为![]() .
.
②对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如表表格:
的图象可以得到如表表格:
|
|
|
|
| + | ﹣ | + |
由表格可知不等式![]() 的解集为 .
的解集为 .
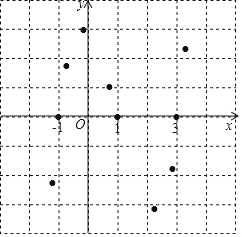
③对于不等式![]() ,请根据已描出的点画出函数
,请根据已描出的点画出函数![]() (x+1)的图象;
(x+1)的图象;
观察函数![]() 的图象补全下面的表格:
的图象补全下面的表格:
|
|
|
|
|
| + | ﹣ |
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
……
小明将上述探究过程总结如下:对于解形如![]() (
(![]() 为正整数)的不等式,先将
为正整数)的不等式,先将![]() 按从大到小的顺序排列,再划分
按从大到小的顺序排列,再划分![]() 的范围,然后通过列表格的办法,可以发现表格中
的范围,然后通过列表格的办法,可以发现表格中![]() 的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
(2)请你参考小明的方法解决下列问题:
①不等式![]() 的解集为 .
的解集为 .
②不等式![]() 的解集为 .
的解集为 .