题目内容
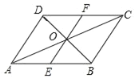
【题目】如图1,正△ABC中,点D为BC边的中点,将∠ACB绕点C顺时针旋转α角度(0°<α<60°)得∠A'CB',点P为线段A′C上的一点,连接PD与B′C、AC分别交点点E、F,且∠PAC=∠EDC.
(1)求证:AP=2ED;
(2)猜想PA和PC的位置关系,并说明理由;
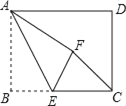
(3)如图2,连接AD交B'C于点G,若AP=2,PC=4,求AG的长.

【答案】(1)详见解析;(2)PA⊥PC.(3)![]() -
-![]() .
.
【解析】
(1)易证得△CDE∽△CAP,得到![]() ,即可证得结论;
,即可证得结论;
(2)先证得A、D、C、P四点共圆,即可证得AC是共圆的直径,根据圆周角定理看证得∠APC=90°;
(3)根据勾股定理求得等边三角形ABC的边长,由(1)的结论求得DE=1,根据勾股定理求得EC,然后通过证得△EDG∽△ECD,得到![]() ,进而即可求得AG的长.
,进而即可求得AG的长.
(1)证明:∵将∠ACB绕点C顺时针旋转α角度(0°<α<60°)得∠A'CB',
∴∠DCE=∠ACP,
∵∠PAC=∠EDC,
∴△CDE∽△CAP,
∴![]() =
=![]() ,
,
∵△ABC 是等边三角形,
∴BC=AC,
∴点D为BC边的中点,
∴CD=![]() BC=
BC=![]() AC,
AC,
∴![]() =
=![]() =
=![]() ,
,
∴AP=2ED;
(2)解:PA⊥PC,
理由:连接AD,如图1,
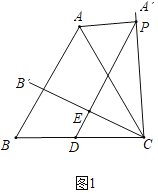
∵△ABC是等边三角形,BD=CD,
∴AD⊥BC,
∴∠ADC=90°,
∵∠PAC=∠EDC,
∴A、D、C、P四点共圆,
∵∠ADC=90°,
∴AC是共圆的直径,
∴∠APC=90°,
∴PA⊥PC;
(3)解:如图2,

∵AP=2,PC=4,∠APC=90°,
∴AC=![]() =2
=2![]() ,
,
∴DC=![]() AC=
AC=![]() ,AD=
,AD=![]() AC=
AC=![]()
∵AP=2ED,
∴ED=1,
∵△CDE∽△CAP,
∴∠CED=∠APC=90°,
∴CE=![]() =2,
=2,
∵∠EDG+∠EDC=90°∠EDC+∠ECD=90°,
∴∠EDG=∠ECD,
∵∠CED=∠DEG=90°,
∴△EDG∽△ECD,
∴![]() =
=![]() ,
,
∴GD=![]() =
=![]() =
=![]() ,
,
∴AG=AD-GD=![]() -
-![]() .
.

【题目】某校为了解本校九年级学生的数学作业完成情况,将完成情况分为四个等级:
等级 | A | B | C | D |
情况分类 | 好 | 较好 | 一般 | 不好 |
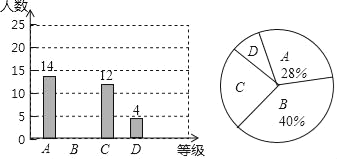
随机对该年级若干名学生进行了调查,然后把调查结果绘制成两幅不完整的统计图.请根据图中的信息解答下列问题:
(1)补全条形统计图;
(2)该年级共有700人,估计该年级数学作业完成等级为D等的人数;
(3)在此次调查中,有甲、乙、丙、丁四个班的学生数学作业完成表现出色,现决定从这四个班中随机选取两个班在全校举行一次数学作业展览,请用画树状图或列表的方法,求恰好选到甲、乙两个班的概率.
【题目】某学校八年级学生学习《从数据谈节水》后,积极响应“节约用水,从我做起”的号召,下列是10名学生统计各自家族一个月的节水情况:
节水量(m3) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
家族数(个) | 1 | 2 | 2 | 4 | 1 |
那么这组数据的众数和中位数分别是( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()