题目内容
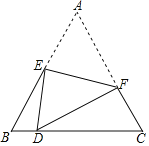
【题目】在等边△ABC中,AB=5,点D为BC上一点,BD:DC=1:4.点E和点F分别是AB、AC边上的点,将△AEF沿EF折叠,使点A刚好落在点D处,则AF=_____.
【答案】![]() .
.
【解析】
设AF=x,由等边三角形的性质得出BC=AC=AB=5,∠B=∠C=∠A=60°,求出BD=1,CD=4,由折叠的性质得:AE=DE,AF=DF=x,∠EDF=∠A=60°=∠B,由三角形的外角性质得出∠BED=∠CDF,证明△BDE∽△CFD,得出BE=![]() ,DE=
,DE=![]() ,由AE+BE=AB=5得出方程,解方程即可.
,由AE+BE=AB=5得出方程,解方程即可.
解:设AF=x,
∵△ABC是等边三角形,
∴BC=AC=AB=5,∠B=∠C=∠A=60°,
∵BD:DC=1:4,
∴BD=1,CD=4,
由折叠的性质得:AE=DE,AF=DF=x,∠EDF=∠A=60°=∠B,
∵∠EDC=∠CDF+∠EDF=∠BED+∠B,
∴∠BED=∠CDF,
∴△BDE∽△CFD,
∴![]() ,即
,即![]() ,
,
解得:BE=![]() ,DE=
,DE=![]() ,
,
∴AE=DE=![]() ,
,
∵AE+BE=AB=5,
∴![]() +
+![]() =5,
=5,
解得:x=![]() ,即AF=
,即AF=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目