题目内容
【题目】如图,在△ABC中,∠C=90°,AC=BC,∠BAC的平分线AE交BC于点D,且AE⊥BE. 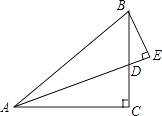
(1)求∠DBE的大小;
(2)求证:AD=2BE.
【答案】
(1)解:∵∠C=90°,AC=BC,
∴∠BAC=45°,
∵AE是∠BAC的平分线,
∴∠CAD= ![]() ∠BAC=22.5°,
∠BAC=22.5°,
∵AE⊥BE,
∴∠BED=90°,
∴∠ACD=∠BED=90°,∵∠ADC=∠BDE,
∴∠DBE=∠CAD=22.5°
(2)证明:延长AC、BE交于点G.
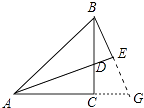
∵AE⊥BG,
∴∠AEB=∠AEG=90°,
在△AEB和△AEG中,
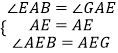 ,
,
∴△AEB≌△AEG,
∴BE=EG,
在△ACD和△BCG中,
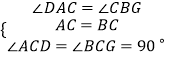 ,
,
∴△ACD≌△BCG,
∴AD=BG=2BE,
∴AD=2BE.
【解析】(1)求出∠CAD,再证明∠DBE=∠CAD即可.(2)先证明△AEB≌△AEG,推出BE=EG,再证明△ACD≌△BCG,推出AD=BG,由此即可证明.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.

练习册系列答案
相关题目

