题目内容
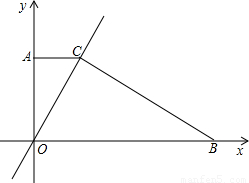
如图,直角坐标系内的梯形AOBC(O为原点)中AC∥OB,AO⊥OB,AC=1,OA=2,OB=5.(1)求经过O,C,B三点的抛物线的解析式;
(2)延长AC交抛物线于点D,求线段CD的长;
(3)在(2)的条件下,动点P、Q分别从O、D同时出发,都以每秒1个单位的速度运动,其中点P沿OB由O向B运动,点Q沿DC由D由C运动(其中一个点运动到终点后,另一个点运动也随之停止),过点Q作QM⊥CD交BC于点M,连接PM.设动点运动的时间为t秒,请你探索:当时间t为何值时,△PMB中有一个角是直角.
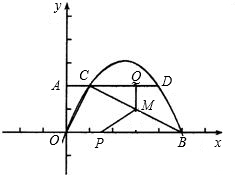
分析:(1)由于抛物线经过原点,因此可以设解析式为y=ax2+bx,再把B、C两点的坐标代入抛物线即可求出二次函数的解析式.
(2)本题可以根据C、D两点的纵坐标相等,求出D点的横坐标,则C、D两点之差即为所求.
(3)由题意可知,△PMB有一个角是直角有两种情况①∠MPB=90°时,此时Q、M、P三点在一条直线上,根据四边形AOPQ为矩形,求出t;②∠PMB=90°时,延长QM交X轴于点N,△PNM∽△MNB,△CQM∽△BNM,求出t.
(2)本题可以根据C、D两点的纵坐标相等,求出D点的横坐标,则C、D两点之差即为所求.
(3)由题意可知,△PMB有一个角是直角有两种情况①∠MPB=90°时,此时Q、M、P三点在一条直线上,根据四边形AOPQ为矩形,求出t;②∠PMB=90°时,延长QM交X轴于点N,△PNM∽△MNB,△CQM∽△BNM,求出t.
解答:解:(1)由题意知,O(0,0),C(1,2),B(5,0).
设过O、C、B三点的抛物线的解析式为y=ax2+bx,
将C、B点坐标代入y=ax2+bx,得
可得
∴y=-
x2+
x.
(2)当y=2时,则-
x2+
x=2,
解得,x1=1,x2=4.
∴CD=4-1=3;
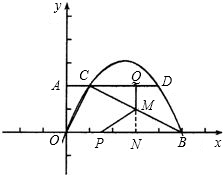
(3)延长QM交x轴于点N,有MN⊥OB.
①当点P与点N重合时,有
MP⊥OB,则四边形AOPQ是矩形.
∴AQ=OP即4-t=t
∴t=2.
②若MP⊥BM,则△PNM∽△MNB.
∴MN2=PN•BN.
∵CQ∥NB,
∴△CQM∽△BNM.
∴
=
,
即
=
,
则MN=
.
∵BN=1+t,PN=5-(1+t)-t=4-2t,
∴(
) 2=(4-2t)(t+1).
解得,t1=-1(舍去),t2=
,
综合①,②知,当t=2或t=
时,△PMB中有一个角是直角.
设过O、C、B三点的抛物线的解析式为y=ax2+bx,
将C、B点坐标代入y=ax2+bx,得
|
可得
|
∴y=-
| 1 |
| 2 |
| 5 |
| 2 |
(2)当y=2时,则-
| 1 |
| 2 |
| 5 |
| 2 |
解得,x1=1,x2=4.
∴CD=4-1=3;

(3)延长QM交x轴于点N,有MN⊥OB.
①当点P与点N重合时,有
MP⊥OB,则四边形AOPQ是矩形.
∴AQ=OP即4-t=t
∴t=2.
②若MP⊥BM,则△PNM∽△MNB.
∴MN2=PN•BN.
∵CQ∥NB,
∴△CQM∽△BNM.
∴
| MN |
| MQ |
| BN |
| CQ |
即
| MN |
| 2-MN |
| 5-(4-t) |
| 4-1-t |
则MN=
| t+1 |
| 2 |
∵BN=1+t,PN=5-(1+t)-t=4-2t,
∴(
| t+1 |
| 2 |
解得,t1=-1(舍去),t2=
| 5 |
| 3 |
综合①,②知,当t=2或t=
| 5 |
| 3 |
点评:本题主要考查了待定系数法求二次函数解析式、在坐标系中两点间的距离,相似三角形等知识.主要考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
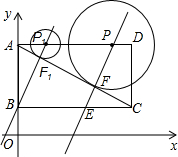 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为AD边上一动点(与点A、D不重合),以点P为圆心作⊙P与对角线AC相切于点F,过P、F作直线L,交BC边于点E,当点P运动到点P1位置时,直线L恰好经过点B,此时直线的解析式是y=2x+1.
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为AD边上一动点(与点A、D不重合),以点P为圆心作⊙P与对角线AC相切于点F,过P、F作直线L,交BC边于点E,当点P运动到点P1位置时,直线L恰好经过点B,此时直线的解析式是y=2x+1.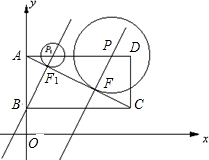 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为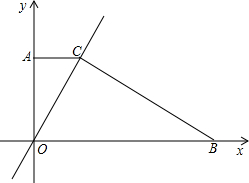
 S梯形AOBC?若存在,请直接写出M点的坐标;若不存在,说明理由.
S梯形AOBC?若存在,请直接写出M点的坐标;若不存在,说明理由.