题目内容
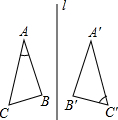
如图，把矩形纸片ABCD沿着EF折叠，使点B落在边AD上的点D处．点A落在点A′．
（1）试说明DE=BF；
（2）若AB=6，AD=8，求AE的长．
（1）试说明DE=BF；
（2）若AB=6，AD=8，求AE的长．
（1）证明：∵把矩形纸片ABCD沿着EF折叠，使点B落在边AD上的点D处，点A落在点A′．
∴∠2=∠3，∠1=∠3，
∴∠1=∠2，
∴DE=DF，
∵DF=BF，
∴DE=BF；
（2）设AE=x，则A′E=x，DE=8-x，
∵A′D 2+A′E 2=DE 2，
∴6 2+x 2=（8-x） 2，
解得：x=
，
即AE的长为
．
∴∠2=∠3，∠1=∠3，
∴∠1=∠2，
∴DE=DF，
∵DF=BF，
∴DE=BF；
（2）设AE=x，则A′E=x，DE=8-x，
∵A′D 2+A′E 2=DE 2，
∴6 2+x 2=（8-x） 2，
解得：x=
| 7 |
| 4 |
即AE的长为
| 7 |
| 4 |
练习册系列答案
相关题目
180°，得到△AB′C．
