题目内容
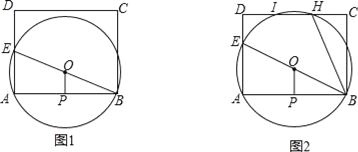
【题目】如图1，已知矩形ABCD，E为AD边上一动点，过A，B，E三点作⊙O，P为AB的中点，连接OP，
（1）求证：BE是⊙O的直径且OP⊥AB；
（2）若AB=BC=8，AE=6，试判断直线DC与⊙O的位置关系，并说明理由；
（3）如图2，若AB=10，BC=8，⊙O与DC边相交于H，I两点，连结BH，当∠ABE=∠CBH时，求△ABE的面积．
【答案】（1）证明见解析；（2）相切，理由见解析；（3）25
【解析】试题分析：（1）利用矩形的性质以及平行线分线段成比例定理得出OP∥AE，AE=2PO，即可得出答案；
（2）首先延长PO交CD于M，求出MO的长等于半径，进而得出答案；
（3）根据题意当∠1=∠2时，可得出tan∠1=tan∠2=tan∠4，设AE=x，CH=y，则DE=8﹣x，DH=10﹣y，可得
=
=
，求出x的值，即可得出答案．
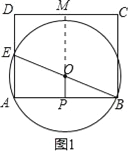
解：（1）如图1，
∵矩形ABCD，∴∠A=90°，∴BE为直径，
∴OE=OB，
∵AP=BP，
∴OP∥AE，AE=2PO，
∴∠OPB=∠A=90°，
即OP⊥AB．
（2）此时直线CD与⊙O相切．
理由：如图1，延长PO交CD于M，
在Rt△ABE中，AB=8，AE=6，
则BE2=62+82=100，
∴BE=10，
∴此时⊙O的半径r=5，∴OM=r=5，
∵在矩形APMD中，PM=AD=8，
∴OM=PM﹣OP=5=r，
∴直线CD与⊙O相切．
（3）如图2，
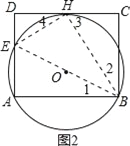
方法I：
∵BE为直径，
∴∠EHB=90°，
∴∠3+∠4=90°，
∵∠C=90°，
∴∠3+∠2=90°，
∴∠2=∠4，
∴当∠1=∠2时，有
tan∠1=tan∠2=tan∠4，
设AE=x，CH=y，则DE=8﹣x，DH=10﹣y，
∴
=
=
，
解得，x=20，或x=5，
∵AE=x＜8，∴x=20，不合题意，舍去，取AE=x=5，
Rt△ABE的面积=
AE×AB=
×5×10=25
方法II：如图3，延长PO交CD于点F，连接OH，
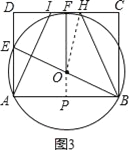
在矩形FPBC，OP⊥AB，且FC=PB=
AB=5，
OP=
AE，OF=8﹣
AE，BE=2HO，
当∠ABE=∠CBH时，设tan∠ABE=tan∠CBH=k时，
在Rt△ABE中，则AE=10tan∠ABE=10k，
在Rt△HBC中，则HC=8tan∠ABE=8k，
∴OP=5k，OF=8﹣5k，FH=5﹣8k，
在Rt△ABE中，BE2=AE2+AB2=100（1+k2），
在Rt△OFH中，HO2=FH2+OF2=（5﹣8k）2+（8﹣5k）2，
∵BE=2HO，∴BE2=4 HO2
∴100（1+k2）=4[（5﹣8k）2+（8﹣5k）2]，
整理得，2 k2﹣5k+2=0，
解得，k=2，或k=
，
当k=2时，AE=10k=20＞8，不合题意，舍去；
当k=
时，AE=10k=5＜8，符合题意，
此时，Rt△ABE的面积=
AE×AB=
×5×10=25．
