题目内容
（1997•武汉）如图，AB为⊙O的直径，C、D是⊙O上的两点，∠BAC=20°， |
| AD |
|
| CD |
分析：由圆周角∠BAC的度数，根据同弧所对的圆心角等于圆周角的2倍，得到圆心角∠BOC的度数，再根据邻补角定义可得出∠AOC的度数，再由
=
，根据等弧对等角，可得∠COD=∠AOD=
∠AOC，进而得到∠COD的度数，再由∠DAC与∠COD所对的弧都为
，根据同弧所对的圆周角等于所对圆心角的一半，可求出∠DAC的度数．
|
| AD |
|
| DC |
| 1 |
| 2 |
|
| DC |
解答：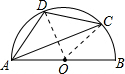
解：连接OC，OD，如图所示：
∵∠BAC与∠BOC所对的弧都为
，∠BAC=20°，
∴∠BOC=2∠BAC=40°，
∴∠AOC=140°，
又
=
，
∴∠COD=∠AOD=
∠AOC=70°，
∵∠DAC与∠DOC所对的弧都为
，
∴∠DAC=
∠COD=35°．
故选C
解：连接OC，OD，如图所示：∵∠BAC与∠BOC所对的弧都为
|
| BC |
∴∠BOC=2∠BAC=40°，
∴∠AOC=140°，
又
|
| AD |
|
| CD |
∴∠COD=∠AOD=
| 1 |
| 2 |
∵∠DAC与∠DOC所对的弧都为
|
| DC |
∴∠DAC=
| 1 |
| 2 |
故选C
点评：此题考查了圆周角定理，以及弦，弧，圆心角三者的关系，要求学生根据题意，作出辅助线，建立未知角与已知角的联系，利用同弧（等弧）所对的圆心角等于所对圆周角的2倍来解决问题．
练习册系列答案
相关题目
（1997•武汉）如图，四边形ABCD内接于圆，则下列结论中正确的是（ ）
（1997•武汉）如图，在Rt△ABC中，∠C=90°，AB=5，BC=3，则sinA=
（1997•武汉）如图，厂房屋顶人字架（等腰三角形）的跨度为10米，∠A=26°，则中柱BC（C为底边中点）的长约是
（1997•武汉）如图，⊙O1与⊙O内切于点A，△ABC内接于⊙O，AB、AC分别交⊙O1于点E和F，BD切⊙O1于点D，且FD是⊙O1的直径，延长FE交BD于点H．