题目内容
【题目】如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10 ,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.
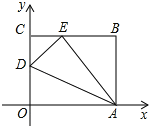
(1)求CE和OD的长;
(2)求直线DE的表达式;
(3)直线y=kx+b与DE平行,当它与矩形OABC有公共点时,直接写出b的取值范围.
【答案】(1)CE=4,OD=5;(2)直线DE的解析式为y=![]() x+5.(3)﹣
x+5.(3)﹣![]() ≤b≤8.
≤b≤8.
【解析】
试题(1)先根据勾股定理求出BE的长,进而可得出CE的长,在Rt△DCE中,由DE=OD及勾股定理可求出OD的长.
(2)根据CE、OD的长求得D、E的坐标,然后根据待定系数法即可求得表达式.
(3)根据平行的性质分析讨论即可求得.
试题解析:(1)依题意可知,折痕AD是四边形OAED的对称轴,
∴在Rt△ABE中,AE=AO=10,AB=8,BE=![]() =6,
=6,
∴CE=10-6=4,
在Rt△DCE中,DC2+CE2=DE2,
又∵DE=OD,
∴(8-OD)2+42=OD2,
∴OD=5.
(2)∵CE=4,
∴E(4,8).
∵OD=5,
∴D(0,5),
设直线DE的解析式为y=mx+n,
∴![]() ,解得
,解得 ,
,
∴直线DE的解析式为y=![]() x+5.
x+5.
(3)∵直线y=kx+b与DE平行,
∴直线为y=![]() x+b,
x+b,
∴当直线经过A点时,0=![]() ×10+b,则b=-
×10+b,则b=-![]() ,
,
当直线经过C点时,则b=8,
∴当直线y=kx+b与矩形OABC有公共点时,-![]() ≤b≤8.
≤b≤8.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案【题目】某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
劳动时间(时) | 频数(人数) | 频率 |
0.5 | 12 | 0.12 |
1 | 30 | 0.3 |
1.5 | x | 0.5 |
2 | 8 | y |
合计 | m | 1 |
(1)统计表中的m= ,x= ,y= ;
(2)被抽样调查的同学劳动时间的众数是 ,中位数是 ;
(3)请将条形图补充完整;
(4)求所有被调查同学的平均劳动时间.