题目内容
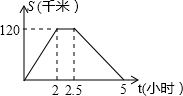 一辆汽车从甲地开往乙地,到达乙地休息了一段时间后再返回甲地.设该汽车从甲地出发的时间t(小时),汽车离甲地的距离为S(千米),且S与t的之间的函数关系如图所示,根据图象信息,解答下列问题:
一辆汽车从甲地开往乙地,到达乙地休息了一段时间后再返回甲地.设该汽车从甲地出发的时间t(小时),汽车离甲地的距离为S(千米),且S与t的之间的函数关系如图所示,根据图象信息,解答下列问题:
(1)这辆汽车的往、返速度是否相同?请说明理由.
(2)求返程中S与t之间的函数关系式.
(3)求这辆汽车从甲地出发时间为t=4时,与甲地的距离是多少?
解:(1)由函数图象得,这辆车的往返速度不同.
理由:从甲地到乙地所用的时间是2小时,平均速度是120÷2=60km/时,从乙地到甲地所用时间是2.5小时,平均速度是120÷2.5=48km/时,60≠48,
所以往返速度不一样;
(2)设返程中S与t之间的函数关系式为S=kt+b,由函数图象,得
 ,
,
解得: ,
,
故返程中S与t之间的函数关系式为:S=-48t+240(2.5≤t≤5);
(3)当t=4时,S=-48×4+240=48.
故这辆汽车从甲地出发时间为t=4时,与甲地的距离是48km.
分析:(1)由函数图象可以得出去时用的时间是2小时,回来用的时间是2.5小时,故可以得出速度不相同;
(2)设返程中S与t之间的函数关系式为S=kt+b,运用待定系数法求出其解即可;
(3)当t=4时带入(2)的解析式就可以求出离甲地的距离.
点评:本题考查了待定系数法求一次函数的解析式的运用,由解析式根据自变量的值求函数值的运用.解答本题时求出函数的解析式是关键.
理由:从甲地到乙地所用的时间是2小时,平均速度是120÷2=60km/时,从乙地到甲地所用时间是2.5小时,平均速度是120÷2.5=48km/时,60≠48,
所以往返速度不一样;
(2)设返程中S与t之间的函数关系式为S=kt+b,由函数图象,得
 ,
,解得:
 ,
,故返程中S与t之间的函数关系式为:S=-48t+240(2.5≤t≤5);
(3)当t=4时,S=-48×4+240=48.
故这辆汽车从甲地出发时间为t=4时,与甲地的距离是48km.
分析:(1)由函数图象可以得出去时用的时间是2小时,回来用的时间是2.5小时,故可以得出速度不相同;
(2)设返程中S与t之间的函数关系式为S=kt+b,运用待定系数法求出其解即可;
(3)当t=4时带入(2)的解析式就可以求出离甲地的距离.
点评:本题考查了待定系数法求一次函数的解析式的运用,由解析式根据自变量的值求函数值的运用.解答本题时求出函数的解析式是关键.

练习册系列答案
相关题目
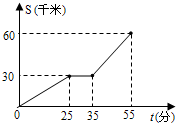 如图反映了一辆汽车从甲地开往乙地的过程中,汽车离开甲地的距离s(千米)与所用时间t(分)之间的函数关系.已知汽车在途中停车加油一次,根据图象,下列描述中,不正确的是( )
如图反映了一辆汽车从甲地开往乙地的过程中,汽车离开甲地的距离s(千米)与所用时间t(分)之间的函数关系.已知汽车在途中停车加油一次,根据图象,下列描述中,不正确的是( )| A、汽车在途中加油用了10分钟 | B、汽车在加油前后,速度没有变化 | C、汽车加油后的速度为每小时90千米 | D、甲乙两地相距60千米 |