题目内容
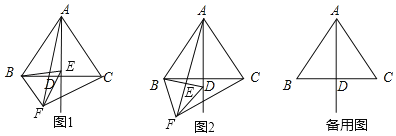
【题目】已知△ABC是等边三角形,AD⊥BC于点D,点E是直线AD上的动点,将BE绕点B顺时针方向旋转60°得到BF,连接EF、CF、AF.
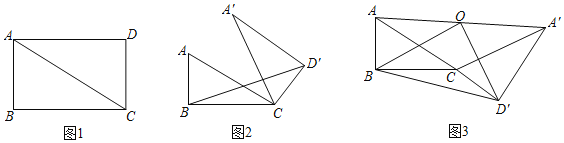
(1)如图1,当点E在线段AD上时,猜想∠AFC和∠FAC的数量关系;(直接写出结果)
(2)如图2,当点E在线段AD的延长线上时,(1)中的结论还成立吗?若成立,请证明你的结论,若不成立,请写出你的结论,并证明你的结论;
(3)点E在直线AD上运动,当△ACF是等腰直角三角形时,请直接写出∠EBC的度数.
【答案】(1)∠AFC+∠FAC=90°,见解析;(2)仍成立,见解析;(3)15°
【解析】
(1)由旋转的性质可得BE=BF,∠EBF=60°,由“SAS”可证△ABE≌△CBF,可得∠BAE=∠BCF=30°,由直角三角形的性质可得结论;
(2)由旋转的性质可得BE=BF,∠EBF=60°,由“SAS”可证△ABE≌△CBF,可得∠BAE=∠BCF=30°,由直角三角形的性质可得结论;
(3)由全等三角形的性质和等边三角形的性质可得AB=AE,由等腰三角形的性质可求解.
解:(1)∠AFC+∠FAC=90°,
理由如下:连接AF,
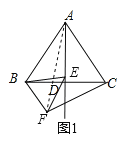
∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠BAC=∠ACB=60°,
∵AB=AC,AD⊥BC,
∴∠BAD=30°,
∵将BE绕点B顺时针方向旋转60°得到BF,
∴BE=BF,∠EBF=60°,
∴∠EBF=∠ABC,
∴∠ABE=∠FBC,且AB=BC,BE=BF,
∴△ABE≌△CBF(SAS)
∴∠BAE=∠BCF=30°,
∴∠ACF=90°,
∴∠AFC+∠FAC=90°;
(2)结论仍然成立,
理由如下:∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠BAC=∠ACB=60°,
∵AB=AC,AD⊥BC,
∴∠BAD=30°,
∵将BE绕点B顺时针方向旋转60°得到BF,
∴BE=BF,∠EBF=60°,
∴∠EBF=∠ABC,
∴∠ABE=∠FBC,且AB=BC,BE=BF,
∴△ABE≌△CBF(SAS)
∴∠BAE=∠BCF=30°,
∴∠ACF=90°,
∴∠AFC+∠FAC=90°;
(3)∵△ACF是等腰直角三角形,
∴AC=CF,
∵△ABE≌△CBF,
∴CF=AE,
∴AC=AE=AB,
∴∠ABE=![]() =75°,
=75°,
∴∠EBC=∠ABE﹣∠ABC=15°.

【题目】如图,![]() 是直径AB所对的半圆弧,点C在
是直径AB所对的半圆弧,点C在![]() 上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.
上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.
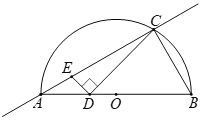
小明根据学习函数的经验,对线段AE,AD长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点D在AB上的不同位置,画图、测量,得到线段AE,AD长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | ||
AE/cm | 0.00 | 0.41 | 0.77 | 1.00 | 1.15 | 1.00 | 0.00 | 1.00 | 4.04 | … |
AD/cm | 0.00 | 0.50 | 1.00 | 1.41 | 2.00 | 2.45 | td style="width:10%; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">3.21 | 3.50 | … |
在AE,AD的长度这两个量中,确定_______的长度是自变量,________的长度是这个自变量的函数;
(2)在下面的平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
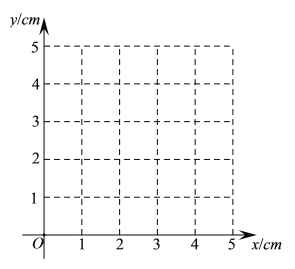
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为________cm(结果精确到0.1).
AD时,AD的长度约为________cm(结果精确到0.1).