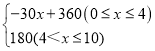题目内容
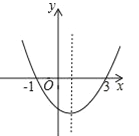
【题目】如图，二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-1，3，则下列结论正确的个数有（ ）①ac＜0；②2a+b=0；③4a+2b+c＞0；④对于任意x均有ax2+bx≥a+b．
A．1 B．2 C．3 D．4
【答案】C.
【解析】
试题解析：：根据图象可得：抛物线开口向上，则a＞0．抛物线与y交与负半轴，则c＜0，
故①ac＜0错误；
对称轴：x=-
＞0，
∵它与x轴的两个交点分别为（-1，0），（3，0），
∴对称轴是x=1，
∴-=1，
∴b+2a=0，
故②2a+b=0正确；
把x=2代入y=ax2+bx+c=4a+2b+c，由图象可得4a+2b+c＞0，
故③4a+2b+c＞0正确；
对于任意x均有ax2+bx≥a+b，
故④正确；
故选C.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某校九年级一班全体学生2017年中招理化生实验操作考试的成绩统计如下表，根据表中的信息判断，下列结论中错误的是（ ）
成绩（分） | 30 | 29 | 28 | 26 | 18 |
人数（人） | 32 | 4 | 2 | 1 | 1 |
A. 该班共有40名学生
B. 该班学生这次考试成绩的平均数为29.4分
C. 该班学生这次考试成绩的众数为30分
D. 该班学生这次考试成绩的中位数为28分
