题目内容
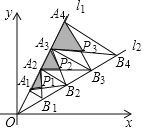
【题目】如图,A1,A2,A3…,An,An+1是直线![]() 上的点,且OA1=A1A2=A2A3=…AnAn+1=2,分别过点A1,A2,A3…,An,An+1作l1的垂线与直线
上的点,且OA1=A1A2=A2A3=…AnAn+1=2,分别过点A1,A2,A3…,An,An+1作l1的垂线与直线![]() 相交于点B1,B2,B3…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3…,AnBn+1,BnAn+1,交点依次为P1,P2,P3…,Pn,设△P1A1A2,△P2A2A3,△P3A3A4,…,△PnAnAn+1的面积分别为S1,S2,S3…,Sn,则Sn=______.(用含有正整数n的式子表示)
相交于点B1,B2,B3…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3…,AnBn+1,BnAn+1,交点依次为P1,P2,P3…,Pn,设△P1A1A2,△P2A2A3,△P3A3A4,…,△PnAnAn+1的面积分别为S1,S2,S3…,Sn,则Sn=______.(用含有正整数n的式子表示)
【答案】![]()
![]()
【解析】
设△OA1B1的面积为S.由OA1=A1A2=A2A3=…AnAn+1,A1B1∥A2B2∥A3B3∥…∥AnBn,推出A1B1:A2B2:A3B3:…:AnBn=1:2:3:…:n,推出![]() =S,
=S,![]() =2S,…,
=2S,…,![]() =nS,探究规律,利用规律即可解决问题;
=nS,探究规律,利用规律即可解决问题;
设△OA1B1的面积为S.
由题意可知OA1=A1A2=A2A3=…AnAn+1,A1B1∥A2B2∥A3B3∥…∥AnBn,
∴A1B1:A2B2:A3B3:…:AnBn=1:2:3:…:n,
∴![]() =S,
=S,![]() =2S,…,
=2S,…,![]() =nS,
=nS,
∴S1=![]() S,S2=
S,S2=![]() 2S,S3=
2S,S3=![]() 3S,…,Sn=
3S,…,Sn=![]() nS,
nS,
∵直线![]() 上的点,直线
上的点,直线![]() ,
,
∴两条直线与x轴的夹角分别为60°和30°,
∴∠A1OB1=30°,
∵OA1=2,
∴A1B1=![]()
∴S=![]()
∴Sn=![]()
![]() ,
,
故答案为:![]()
![]() .
.

【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?