Question

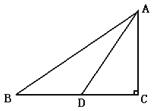
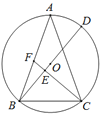
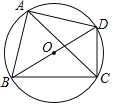
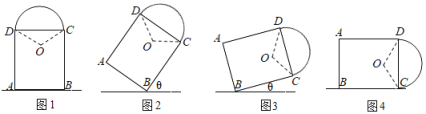
【题目】如图1，一艺术拱门由两部分组成，下部为矩形ABCD，AB，AD的长分别是2m和4m，上部是圆心为O的劣弧CD，圆心角∠COD＝120°．现欲以B点为支点将拱门放倒，放倒过程中矩形ABCD所在的平面始终与地面垂直，如图2、图3、图4所示记拱门上的点到地面的最大距离hm，则h的最大值为___m．

Answer 1

【答案】（2+2）．

【解析】

利用勾股定理先求出圆弧的半径，然后分析出h取得最大值时为OB与地面垂直时，从而可解．

解：如图所示，过点O作垂直于地面的直线与拱门外框上沿交于点P，交地面于点Q，

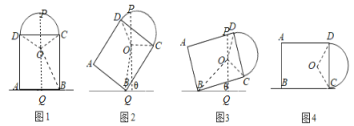
如图1，AB，AD的长分别是2m和4m，圆心角∠COD＝120°，

∴∠DOP＝60°，DC＝AB＝，

∴OD＝2，PQ＝5，

当点P在线段AD上时，拱门上的点到地面的最大距离h等于点D到地面的距离，即点P与点D重合时，此时

h＝，

如图2所示，当点P在劣弧CD上时，拱门上的点到地面的最大距离h等于⊙O的半径长与圆心O到地面的距离之和，

易知，OQ≤OB，

而h＝OP+OQ＝2+OQ，

∴当点Q与点B重合时，h取得最大值，

由图1可知，OQ＝3，BQ＝，则OB＝，

h的最大值为OP+OB，即2+．

故答案为：（2+）．