题目内容
【题目】已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y= ![]() (x>0)经过D点,交BC的延长线于E点,且OBAC=160,则点E的坐标为( )
(x>0)经过D点,交BC的延长线于E点,且OBAC=160,则点E的坐标为( )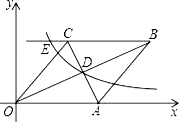
A.(5,8)
B.(5,10)
C.(4,8)
D.(3,10)
【答案】C
【解析】解:过点C作CF⊥x轴于点F,
∵OBAC=160,A点的坐标为(10,0),
∴OACF= ![]() OBAC=
OBAC= ![]() ×160=80,菱形OABC的边长为10,
×160=80,菱形OABC的边长为10,
∴CF= ![]() =
= ![]() =8,
=8,
在Rt△OCF中,
∵OC=10,CF=8,
∴OF= ![]() =
= ![]() =6,
=6,
∴C(6,8),
∵点D时线段AC的中点,
∴D点坐标为( ![]() ,
, ![]() ),即(8,4),
),即(8,4),
∵双曲线y= ![]() (x>0)经过D点,
(x>0)经过D点,
∴4= ![]() ,即k=32,
,即k=32,
∴双曲线的解析式为:y= ![]() (x>0),
(x>0),
∵CF=8,
∴直线CB的解析式为y=8,
∴ 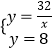 ,
,
解得: ![]() ,
,
∴E点坐标为(4,8).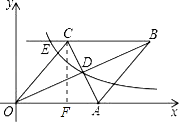
【考点精析】本题主要考查了菱形的性质的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目