题目内容
△ABC中,点D、E分别在AB、AC上,且DE∥BC,AE=1,EC=2,则S△ABC:S△ADE=
- A.2:1
- B.3:1
- C.4:1
- D.9:1
D
分析:由于DE∥BC,易证得△ABC∽△ADE,则它们的面积比等于相似比的平方,由此得解.
解答:∵AE=1,CE=2,
∴AC=AE+CE=3=3AE;
∵DE∥BC,
∴△ABC∽△ADE;
∴S△ABC:S△ADE=AC2:AE2=9:1;
故选D.
点评:此题主要考查的是相似三角形的性质:相似三角形的面积比等于相似比的平方.
分析:由于DE∥BC,易证得△ABC∽△ADE,则它们的面积比等于相似比的平方,由此得解.
解答:∵AE=1,CE=2,
∴AC=AE+CE=3=3AE;
∵DE∥BC,
∴△ABC∽△ADE;
∴S△ABC:S△ADE=AC2:AE2=9:1;
故选D.
点评:此题主要考查的是相似三角形的性质:相似三角形的面积比等于相似比的平方.

练习册系列答案
相关题目
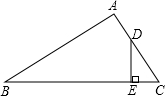 如图,在△ABC中,点D在AC上,DE⊥BC,垂足为E,若AD=2DC,AB=4DE,则sinB等于( )
如图,在△ABC中,点D在AC上,DE⊥BC,垂足为E,若AD=2DC,AB=4DE,则sinB等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
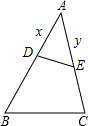 如图,在△ABC中,点D在AB上,点E在AC上,若∠ADE=∠C,且AB=5,AC=4,AD=x,AE=y,则y与x的关系式是( )
如图,在△ABC中,点D在AB上,点E在AC上,若∠ADE=∠C,且AB=5,AC=4,AD=x,AE=y,则y与x的关系式是( )| A、y=5x | ||
B、y=
| ||
C、y=
| ||
D、y=
|
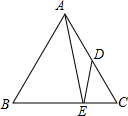 如图,在正△ABC中,点D是AC的中点,点E在BC上,且
如图,在正△ABC中,点D是AC的中点,点E在BC上,且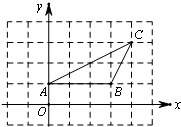 15、如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),回答下列问题(直接写出结果):
15、如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),回答下列问题(直接写出结果):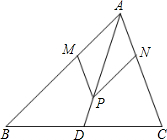 如图,在△ABC中,点D为BC上一点,点P在AD上,过点P作PM∥AC交AB于点M,作PN∥AB交AC于点N.
如图,在△ABC中,点D为BC上一点,点P在AD上,过点P作PM∥AC交AB于点M,作PN∥AB交AC于点N.