ƒøƒĞ»ı
°æƒø°ø»ÁÕº£¨‘Ğ∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨“—÷™÷±œşAB£∫y= ![]() x+4Ωªx÷·”е„A£¨Ωªy÷·”е„B£Æ÷±œşCD£∫y=©Å
x+4Ωªx÷·”е„A£¨Ωªy÷·”е„B£Æ÷±œşCD£∫y=©Å ![]() x©Å1”Î÷±œşABœ‡Ωª”е„M£¨Ωªx÷·”е„C£¨Ωªy÷·”е„D£Æ
x©Å1”Î÷±œşABœ‡Ωª”е„M£¨Ωªx÷·”е„C£¨Ωªy÷·”е„D£Æ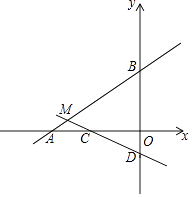
£®1£©÷±Ω”–¥≥ˆµ„B∫Õµ„Dµƒ◊¯±Í£ª
£®2£©»Ùµ„P «…‰œşMD…œµƒ“ª∏ˆ∂ص„£¨…˵„Pµƒ∫·◊¯±Í «x£¨°˜PBMµƒ√ʪ˝ «S£¨«ÛS”Îx÷ƺ‰µƒ∫Ø ˝πÿœµ£ª
£®3£©µ±S=20 ±£¨∆Ω√Ê÷±Ω«◊¯±ÍœµƒĞ «∑ҥʑе„E£¨ π“‘µ„B°¢E°¢P°¢MŒ™∂•µ„µƒÀƒ±ş–Œ «∆Ω––Àƒ±ş–Œ£ø»Ù¥Ê‘Ğ£¨«Î÷±Ω”–¥≥ˆÀ˘”–∑˚∫œÃº˛µƒµ„Eµƒ◊¯±Í£ª»Ù≤ª¥Ê‘Ğ£¨Àµ√˜¿Ì”…£Æ
°æ¥∞∏°ø
£®1£©Ω‚£∫°şµ„B «÷±œşAB£∫y= ![]() x+4”Îy÷·µƒΩªµ„◊¯±Í£¨
x+4”Îy÷·µƒΩªµ„◊¯±Í£¨
°‡B£®0£¨4£©£¨
°şµ„D «÷±œşCD£∫y=©Å ![]() x©Å1”Îy÷·µƒΩªµ„◊¯±Í£¨
x©Å1”Îy÷·µƒΩªµ„◊¯±Í£¨
°‡D£®0£¨©Å1£©£ª
£®2£©Ω‚£∫»ÁÕº1£¨°ş÷±œşAB”ÎCDœ‡Ωª”ĞM£¨
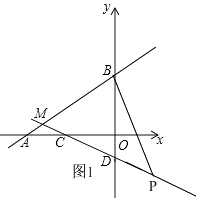
°‡M£®©Å5£¨ ![]() £©£¨
£©£¨
°şµ„Pµƒ∫·◊¯±ÍŒ™x£¨
°‡µ„P£®x£¨©Å ![]() x©Å1£©£¨
x©Å1£©£¨
°şB£®0£¨4£©£¨D£®0£¨©Å1£©£¨
°‡BD=5£¨
°şµ„P‘Ğ…‰œşMD…œ£¨º¥£∫x°ı0 ±£¨
S=S°˜BDM+S°˜BDP= ![]() °¡5£®5+x£©=
°¡5£®5+x£©= ![]() x+
x+ ![]() £¨
£¨
£®3£©Ω‚£∫»ÁÕº£¨”…£®1£©÷™£¨S= ![]() x+
x+ ![]() £¨
£¨
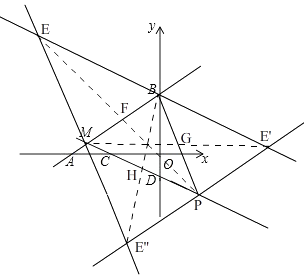
µ±S=20 ±£¨ ![]() x+
x+ ![]() =20£¨
=20£¨
°‡x=3£¨
°‡P£®3£¨©Å2£©£¨
¢Ÿµ±BP «∂‘Ω«œş ±£¨»°BPµƒ÷–µ„G£¨¡¨Ω”MG≤¢—”≥§»°“ªµ„E' πGE'=GE£¨
…ËE'£®m£¨n£©£¨
°şB£®0£¨4£©£¨P£®3£¨©Å2£©£¨
°‡BPµƒ÷–µ„◊¯±ÍŒ™£® ![]() £¨1£©£¨
£¨1£©£¨
°şM£®©Å5£¨ ![]() £©£¨
£©£¨
°‡ ![]() =
= ![]() £¨
£¨ ![]() =1£¨
=1£¨
°‡m=8£¨n= ![]() £¨
£¨
°‡E'£®8£¨ ![]() £©£¨
£©£¨
¢Ğµ±ABŒ™∂‘Ω«œş ±£¨Õ¨¢Ÿµƒ∑Ω∑®µ√£¨E£®©Å9£¨6£©£¨
¢ğµ±MPŒ™∂‘Ω«œş ±£¨Õ¨¢Ÿµƒ∑Ω∑®µ√£¨E'£®©Å2£¨©Å ![]() £©£¨
£©£¨
º¥£∫¬˙◊„ú˛µƒµ„Eµƒ◊¯±ÍŒ™£®8£¨ ![]() £©°¢£®©Å9£¨6£©°¢£®©Å2£¨©Å
£©°¢£®©Å9£¨6£©°¢£®©Å2£¨©Å ![]() £©£Æ
£©£Æ
°æΩ‚Œˆ°ø£®1£©Ω´x=0¥˙»Î∫Ø ˝Ω‚Œˆ Ωµ√µΩ∂‘”¶µƒy÷µ£¨¥”∂¯ø…µ√µΩµ„B∫Õµ„Dµƒ◊¯±Í£ª
£®2£©Ω´À˘«Û»˝Ω«–Œµƒ√ʪ˝◊™Œ™°˜BDM∫Õ°˜BDPµƒ√ʪ˝÷Æ∫Õ£¨»ª∫Û“¿æı»˝Ω«–Œµƒ√ʪ˝π´ Ω¡–≥ˆ∫Ø ˝πÿœµ Ωº¥ø…£ª
£®3£©∑÷»˝÷÷«Èøˆ¿˚”√∂‘Ω«œşª•œ‡∆Ω∑÷µƒÀƒ±ş–Œ «∆Ω––Àƒ±ş–Œ∫Õœş∂Œµƒ÷–µ„◊¯±Íµƒ»∑∂®∑Ω∑®º¥ø…µ√≥ˆΩ·¬ğ.

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏