题目内容
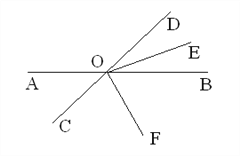
【题目】.如图，直线AB，CD相交于点O ，OE平分∠BOD，OF平分∠COE，∠AOD：∠BOE=4:1，求∠AOF的度数。
【答案】135°
【解析】本题需先根据∠AOD：∠BOE=4:1设∠AOD=4x°，∠BOE=x°，再根据角平分线的性质，分别求出各角的值，再利用角的和差即可求出结果．
解：∵∠AOD：∠BOE=4:1，
∴设∠AOD=4x°，则∠BOE=x°，
∵OE平分∠BOD，
∴∠BOD=2∠BOE=2x°，
∵∠AOD+∠BOD=180°，
∴6x=180，
解得，x=30，
∴∠BOE=30°，∠AOD=120°，∠BOD=60°，
∴∠COE=150°，
∵OF平分∠COE，
∴∠EOF=
∠COE=75°，
∴∠BOF=∠EOF-∠BOE=45°，
∴∠AOF=∠AOB-∠BOF=135°.
练习册系列答案
相关题目
