Question

【题目】已知二次函数.

(1)证明:不论取何值，该函数图像与轴总有公共点;

(2)若该函数的图像与轴交于点(0,3)，求出顶点坐标并画出该函数图像;

(3)在(2)的条件下，观察图像，解答下列问题:

①不等式的的解集是 ;

②若一元二次方程有两个不相等的实数根，则的取值范围是 ;

③若一元二次方程在的范围内有实数根，则的取

值范围是 .

Answer 1

【答案】（1）证明见解析；（2）顶点（1,4）；作图略(3)①0＜x＜2；②k＜4；③-5＜t≤4

【解析】试题分析：（1）令y=0得到关于x的方程，找出相应的a，b及c的值，表示出，整理配方后，根据完全平方式大于等于0，判断出大于等于0，可得出抛物线与x轴总有交点，得证；
（2）由抛物线与y轴交于（0，3），将x=0，y=3代入抛物线解析式，求出m的值，进而确定出抛物线解析式，配方后找出顶点坐标，根据确定出的解析式列出相应的表格，由表格得出7个点的坐标，在平面直角坐标系中描出7个点，然后用平滑的曲线作出抛物线的图象，如图所示；
（3）由图象和解析式即可可求得．

试题解析：(1)

∴不论m取何值，该函数图象与x轴总有公共点，

(2)∵该函数的图象与y轴交于点(0,3)，

∴把x=0，y=3代入解析式得：m=3，

∴顶点坐标为(1,4)；

列表如下：

x	2	1	0	1	2	3	4
y	5	0	3	4	3	0	5

描点；

画图如下：

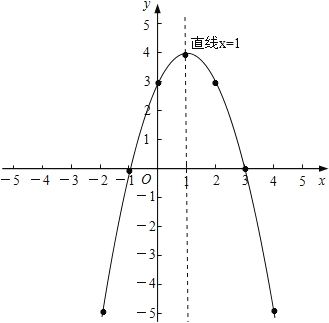
(3)根据图象可知：①不等式的解集是：0<x<2，

②由抛物线的解析式可知若一元二次方程有两个不相等的实数根，则k的取值范围是：k<4，

③若一元二次方程在1<x<4的范围内有实数根,t的取值就是函数在1<x<4的范围内的函数值，由图象可知在1<x<4的范围内，故

故答案为0<x<2，k<4，