题目内容
【题目】如图,把三角形纸片![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在四边形
落在四边形![]() 内部点
内部点![]() 处,
处,
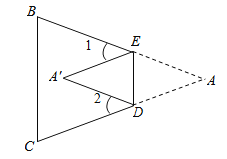
(1)写出图中一对全等的三角形,井写出它们的所有对应角.
(2)设![]() 的度数为
的度数为![]() ,
,![]() 的度数为
的度数为![]() ,那么
,那么![]() 的度数分别是多少(用含
的度数分别是多少(用含![]() 或
或![]() 的式子表示)?
的式子表示)?
(3)![]() 与
与![]() 之间有一种数量关系始终保持不变,请找出这个规律,井说明理由.
之间有一种数量关系始终保持不变,请找出这个规律,井说明理由.
【答案】(1)△AED≌A’ED,∠A和∠A’,∠AED和∠A’ED,∠ADE=∠A’DE;(2)∠1=180°—2x°,∠2=180°—2y°;(3)2∠A=∠1+∠2
【解析】
(1)根据折叠的性质,可得出△ADE≌△A′DE,再根据全等三角形的性质即可得出答案;
(2)由折叠的性质得出,∠1+2∠AED=180°,∠2+2∠ADE=180°,从而得出∠1,∠2的度数;
(3)由折叠的性质得出,∠A=∠A′,再由三角形的内角和定理得出∠A与∠1+∠2的关系.
(1)由折叠的性质得出△ADE≌△A′DE,∠ADE=∠A′DE,∠AED=∠A′ED,∠A=∠A′,
(2)∵∠1+2∠AED=180°,∠2+2∠ADE=180°,
∴∠1=180°-2∠AED,∠2=180°-2∠ADE,
∵∠AED=x,∠ADE=y,
∴∠1=180°-2∠AED=180°-2x,∠2=180°-2∠ADE=180°-2y,
(3)∵∠A′+∠A′DE+∠A′ED=180°,
∴∠A′DE+∠A′ED=180°-∠A′,
∵∠A=∠A′,
∴∠A′DE+∠A′ED=180°-∠A,
∵∠A′DE=∠ADE,∠A′ED=∠AED
∴∠ADE+∠AED=180°-∠A,
∵∠1+2∠AED=180°,∠2+2∠ADE=180°,
∴2(∠AED+∠ADE)=360°-∠1-∠2,
∴∠AED+∠ADE=180°-![]() (∠1+∠2),
(∠1+∠2),
∴∠A=![]() (∠1+∠2),
(∠1+∠2),
∴2∠A=∠1+∠2.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案