Question

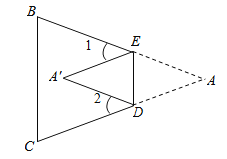
【题目】在△ABC中，AB=1，BC=2，以AC为边作等边三角形ACD，连接BD，则线段BD的最大值为_____．

Answer 1

【答案】3

【解析】

以AB为边作等边△ABE，由题意可证△AEC≌△ABD，可得BD=CE，根据三角形三边关系，可求EC的最大值，即可求BD的最大值．

如图：以AB为边作等边△ABE，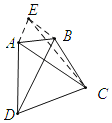
，
∵△ACD，△ABE是等边三角形，
∴AD=AC，AB=AE=BE=1，∠EAB=∠DAC=60o,
∴∠EAC=∠BAD，且AE=AB，AD=AC，
∴△DAB≌△CAE（SAS）
∴BD=CE，
若点E，点B，点C不共线时，EC＜BC+BE；
若点E，点B，点C共线时，EC=BC+BE．
∴EC≤BC+BE=3，
∴EC的最大值为3，即BD的最大值为3.
故答案是：3