题目内容
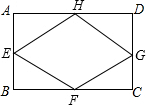
如图,在矩形ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点,若AH:AE=4:3,四边形EFGH的周长是40cm,则矩形ABCD的面积是______cm2.

在△AHE和△DHG中,
∵AH=DH=
AD,∠A=∠D=90°,AE=DG=
AB,
∴△AHE≌△DHG,
∴EH=GH,
同理EH=GH=GF=EF,
即四边形EFGH为菱形.
又∵四边形EFGH的周长是40cm,
∴EH=10.
∵AH:AE=4:3,
设AH=4x,则AE=3x.
由勾股定理得,EH2=AE2+AH2,
∴x=2,AH=8,AE=6,
∴矩形ABCD的面积=16×12=192(cm2).
∵AH=DH=
| 1 |
| 2 |
| 1 |
| 2 |
∴△AHE≌△DHG,
∴EH=GH,
同理EH=GH=GF=EF,
即四边形EFGH为菱形.
又∵四边形EFGH的周长是40cm,
∴EH=10.
∵AH:AE=4:3,
设AH=4x,则AE=3x.
由勾股定理得,EH2=AE2+AH2,
∴x=2,AH=8,AE=6,
∴矩形ABCD的面积=16×12=192(cm2).

练习册系列答案
相关题目