题目内容
如图,已知A、B、C、D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.
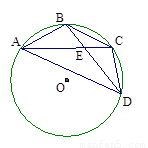
(1)求证:DB平分∠ADC;
(2)若BE=3,ED=6,求A B的长.
【答案】
证明:(1)∵ AB=BC ∴弧AB=弧BC
∴∠BDC=∠ADB, ∴DB平分∠ADC
(2)解:由(1)可知弧AB=弧BC,∴∠BAC=∠ADB
∵∠ABE=∠ABD
∴△ABE∽△DBA
∴=
∵BE=3,ED=6
∴BD=9
∴AB2=BE·BD=3×9=27
∴AB=3
【解析】(1)等弦对等角可证DB平分∠ABC;
(2)易证△ABE∽△DBA,根据相似三角形的性质可求AB的长.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30° 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=