Question

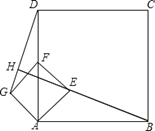
【题目】四边形ABCD、AEFG都是正方形，当正方形AEFG绕点A逆时针旋转45°时，如图，连接DG、BE，并延长BE交DG于点H，且BH⊥DG与H．若AB=4，AE=时，则线段BH的长是 ；

Answer 1

【答案】．

【解析】

连结GE交AD于点N，连结DE，由于正方形AEFG绕点A逆时针旋转45°，AF与EG互相垂直平分，且AF在AD上，由AE=可得到AN=GN=1，所以DN=4﹣1=3，然后根据勾股定理可计算出DG=，则BE=，解着利用S△DEG=GEND=DGHE可计算出HE，所以BH=BE+HE．

解：连结GE交AD于点N，连结DE，如图，

∵正方形AEFG绕点A逆时针旋转45°，

∴AF与EG互相垂直平分，且AF在AD上，

∵AE=，

∴AN=GN=1，

∴DN=4﹣1=3，

在Rt△DNG中，DG==；

由题意可得：△ABE相当于逆时针旋转90°得到△AGD，

∴DG=BE=，

∵S△DEG=GEND=DGHE，

∴HE==，

∴BH=BE+HE=+=．

故答案为．