题目内容
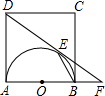如图，以正方形ABCD的AB边为直径，在正方形内部作半圆，圆心为O，DF切半圆于点E，交AB的延长线于点F，BF=4．求：（1）cos∠F的值；（2）BE的长．
分析：（1）解答此题的关键是由△OEF∽△DAF得出AF=2EF，再根据此数值求出EF和FO，然后即可求出cos∠F．
（2）由△BEF∽△EAF，和设BE=k，则AE=2k，即可求得BE．
（2）由△BEF∽△EAF，和设BE=k，则AE=2k，即可求得BE．
解答：解：（1）连接OE，
∵DF切半圆于点E，
∴∠OEF=90°，
∵四边形ABCD为正方形，
∵∠OEF=∠DAF=90°，
∵∠F=∠F，
∴△OEF∽△DAF，
得
=
=
=
，
即AF=2EF，
又EF2=FB•FA=BF•2EF，
∴EF=2BF=8，AF=2EF=16，
∴AB=AF-BF=12，
FO=
AB+BF=10．
cos∠F=
=
；
（2）连接AE，
∵DE是⊙O的切线，
∴∠BEF=∠EAF，
∵∠F为公共角，
∴△BEF∽△EAF，
∴
=
=
=
，
设BE=k，则AE=2k，
根据AB是直径，故∠AEB=90°，
即AE2+BE2=AB2，
得（2k）2+k2=122，
解得k=
，
故BE=
．
∵DF切半圆于点E，
∴∠OEF=90°，
∵四边形ABCD为正方形，
∵∠OEF=∠DAF=90°，
∵∠F=∠F，
∴△OEF∽△DAF，
得
| EF |
| AF |
| OE |
| DA |
| OE |
| AB |
| 1 |
| 2 |
即AF=2EF，
又EF2=FB•FA=BF•2EF，
∴EF=2BF=8，AF=2EF=16，
∴AB=AF-BF=12，
FO=
| 1 |
| 2 |
cos∠F=
| EF |
| FO |
| 4 |
| 5 |
（2）连接AE，
∵DE是⊙O的切线，
∴∠BEF=∠EAF，
∵∠F为公共角，
∴△BEF∽△EAF，
∴
| BE |
| EA |
| EF |
| AF |
| 8 |
| 16 |
| 1 |
| 2 |
设BE=k，则AE=2k，
根据AB是直径，故∠AEB=90°，
即AE2+BE2=AB2，
得（2k）2+k2=122，
解得k=
| 12 |
| 5 |
| 5 |
故BE=
| 12 |
| 5 |
| 5 |
点评：此题涉及的知识点较多，由相似形的判定与性质，勾股定理，正方形的性质等知识点，综合性较强．
练习册系列答案
相关题目
13、如图，以直角△ABC的三边向外作正方形，其面积分别为S1，S2，S3且S1=4，S2=8，则S3=
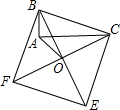如图，以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF，设正方形的中心为O，连接AO，如果AB=4，AO=6
如图，以Rt△ABC的斜边BC为一边作正方形BCDE，设正方形的中心为O，连接AO，如果AB=3，AO=
如图，以Rt△ABC的斜边和一直角边为边长向外作正方形，面积分别为169和25，则另一直角边的长度BC为（ ）
如图，以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3，且S1+S2+S3=50，则AB=（ ）