题目内容
【题目】如图，四边形OABC为矩形，点B坐标为（4，2），A，C分别在x轴，y轴上，点F在第一象限内，OF的长度不变，且反比例函数
经过点F.
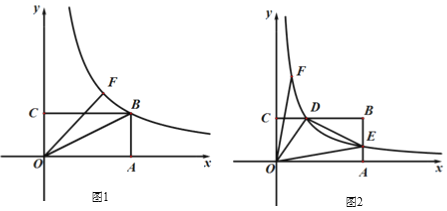
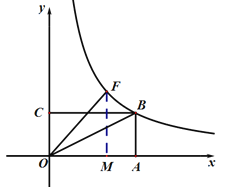
（1）如图1，当F在直线y = x上时，函数图象过点B，求线段OF的长.
（2）如图2，若OF从（1）中位置绕点O逆时针旋转，反比例函数图象与BC，AB相交，交点分别为D，E，连结OD，DE，OE.
①求证：CD=2AE.
②若AE+CD=DE，求k.
③设点F的坐标为（a，b），当△ODE为等腰三角形时，求（a+b）2的值.
【答案】（1）OF =4；（2）①证明见解析；② k=
；③96-16
或36-4.
【解析】分析（1）由y=
经过点B (2,4).，求出k的值，再利用F在直线y = x，求出m的值，最后利用勾股定理求解即可;(2) ①利用反比例函数k的几何意义可求解; ②Rt△EBD中，分别用n表示出BD、BE、DE，再利用勾股定理解答即可; ③分三种情况讨论即可：OE=OD；
OE=DE；OD=DE.
（1）∵F在直线y=x上
∴设F（m，m）
作FM⊥x轴
∴FM=OM=m
∵y=经过点B (2,4).
∴k=8
∴
∴
∴
∴OF =4；
（2）①∵函数
的图象经过点D，E
∴
∵ OC=2，OA=4
∴CO=2AE
②由①得：CD=2AE
∴可设：CD=2n，AE=n
∴DE=CD+AE=3n
BD=4-2n， BE=2-n
在Rt△EBD，由勾股定理得：
∴
解得
③CD=2c，AE=c
情况一：若OD=DE
∴
∴
∴
情况二：若OE=DE
∴
∴
情况三：OE=OD 不存在.
练习册系列答案
快乐5加2金卷系列答案
相关题目
