题目内容
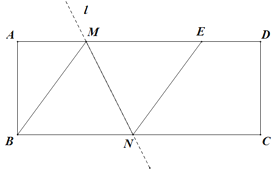
【题目】如图,在矩形ABCD中,AB=4,AD=10,点E在AD边上,已知B、E两点关于直线l对称,直线l分别交AD、BC边于点M、N,连接BM、NE.
(1)求证:四边形BMEN是菱形;
(2)若DE=2,求NC的长.
【答案】(1)证明见解析; (2)NC=5.
【解析】(1)根据B、E两点关于直线l对称,可得BM=ME,BN=NE,再根据矩形的性质可得BM=BN,从而得出BM=ME=BN=NE,通过四边相等的四边形是菱形即可得出结论;(2) 菱形边长为x,利用勾股定理计算即可.
(1)∵ B、E两点关于直线l对称
∴ BM=ME,BN=NE,∠BMN=∠EMN在矩形ABCD中,AD∥BC
∴ ∠EMN=∠MNB
∴ ∠BMN=∠MNB
∴ BM=BN
∴ BM=ME=BN=NE
∴ 四边形ECBF是菱形.
(2)设菱形边长为x
则 AM=8-x
在Rt△ABM中,![]() .
.
∴ x=5. ∴NC=5.

 名校课堂系列答案
名校课堂系列答案【题目】为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
消费卡 | 消费方式 |
普通卡 | 35元/次 |
白金卡 | 280元/张,凭卡免费消费10次再送2次 |
钻石卡 | 560元/张,凭卡每次消费不再收费 |
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用
(Ⅰ)若每年去该健身中心6次,应选择哪种消费方式更合算?
(Ⅱ)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(Ⅲ)若某位顾客每年去该健身中心健身至少18次,请通过计算帮助这位顾客选择最合算的消费方式.
【题目】甲、乙两校派相同人数的优秀学生,参加县教育局举办的中小学生美文诵读决赛。比赛结束后,发现学生成绩分别是7分、8分、9分或10分(满分10分),核分员依据统计数据绘制了如下尚不完整的统计图表。根据这些材料,请你回答下列问题:
甲校成绩统计表 | ||||
成绩 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | 8 | |
(1)在图①中,“7分”所在扇形的圆心角等于_______
(2)求图②中,“8分”的人数,并请你将该统计图补充完整。


(3)经计算,乙校学生成绩的平均数是8.3分,中位数是8分。请你计算甲校学生成绩的平均数、中位数,并从平均数和中位数的角度分析哪个学校的成绩较好?
(4)如果教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?