题目内容
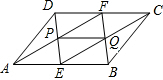 如图,E、F分别是?ABCD的两边AB、CD的中点,AF交DE于P,BF交CE于Q,则PQ与AB的关系是( )
如图,E、F分别是?ABCD的两边AB、CD的中点,AF交DE于P,BF交CE于Q,则PQ与AB的关系是( )| A、PQ∥AB | ||
B、PQ=
| ||
C、PQ∥AB且PQ=
| ||
| D、随?ABCD的形状大小变化而变化 |
考点:平行四边形的性质
专题:几何图形问题
分析:利用已知条件和平行四边形的性质易证△DPF≌△FPA,△FQC≌△BQE,由全等三角形的性质可得:PF=AP,FQ=BQ,所以PQ是△ABF的中位线,由中位线的性质即可得到问题答案.
解答:解:PQ∥AB且PQ=
AB,
理由如下:
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠DFP=∠EAF,
∵E、F分别是?ABCD的两边AB、CD的中点,
∴AE=DF,
在△DPF和△FPA中,
,
∴△DPF≌△FPA(ASA),
∴PF=AP,
同理:△FQC≌△BQE,
∴FQ=BQ,
∴PQ是△ABF的中位线,
∴PQ∥AB且PQ=
AB.
故选C.
| 1 |
| 2 |
理由如下:
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠DFP=∠EAF,
∵E、F分别是?ABCD的两边AB、CD的中点,
∴AE=DF,
在△DPF和△FPA中,
|
∴△DPF≌△FPA(ASA),
∴PF=AP,
同理:△FQC≌△BQE,
∴FQ=BQ,
∴PQ是△ABF的中位线,
∴PQ∥AB且PQ=
| 1 |
| 2 |
故选C.
点评:本题考查了平行四边形的性质、全等三角形的判定和性质以及三角形中位线定理,题目的综合性较强,难度中等.

练习册系列答案
相关题目
小明打算暑假里的某天到上海世博会一日游,上午可以先从台湾馆、香港馆中随机抽一个馆,下午再从加拿大馆、法国馆、俄罗斯馆中随机抽一个馆游玩.则小明恰好上午选中台湾馆,下午选中法国馆这两个场馆的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,PA为⊙0的切线,A为切点,PA=2
如图,PA为⊙0的切线,A为切点,PA=2| 3 |
| A、4 | ||
| B、2 | ||
C、
| ||
| D、1 |
如果关于x的方程
+3=
有增根,则a的值是( )
| a |
| x-2 |
| 1-x |
| 2-x |
| A、2 | B、-2 | C、1 | D、±2 |
下列关于三角形按边分类的集合中,正确的是( )
A、 |
B、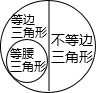 |
C、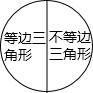 |
D、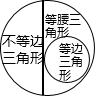 |
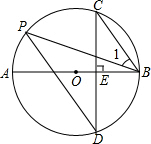 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.