Question

【题目】如图，在△ABC中，AD⊥BC，垂足为D，∠B=60°，∠C=45°．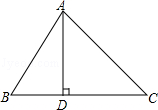
（1）求∠BAC的度数．
（2）若AD=2 ，求AC和AB的长．

Answer 1

【答案】
（1）解：∵在△ABC中，∠B=60°，∠C=45°，

∴∠BAC=180°﹣60°﹣45°=75

（2）解：∵AD⊥BC，

∴△ADC是直角三角形，

又∵∠C=45°，

∴AD=DC，

∴根据勾股定理，得2AD2=AC2，即AC=2 ．

在Rt△ABD中，∵AD=2 ，∠B=60°，

∴AB= =4．

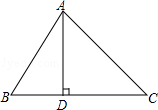
【解析】（1）直接根据三角形内角和定理即可求出∠BAC的度数；（2）先根据∠C=45°判断出△ADC的形状，再由勾股定理即可求出AC，在Rt△ABD中，根据AB= ，即可求出AB．
【考点精析】本题主要考查了勾股定理的概念的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．