��Ŀ����
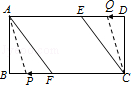
����Ŀ�����ھ���ABCD�У�AB=4��BC=8�������Խ��߽���O��ֱ��EF�Ƶ�O��ת���ֱ�AD��BC�ڵ�E��F������AF��CE��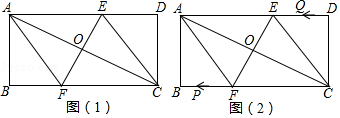
��1����ͼ��1��������������������ͨ�ı��Ρ����Ρ���ͨƽ���ı��Ρ������λ���������ѡ����գ���ת�������ı���AFCEʼ��Ϊ��
����EΪAD���е�ʱ�ı���AFCEΪ��
��EF��ACʱ�ı���AFCEΪ��
��2����ͼ��1������EF��ACʱ����AF�ij���
��3����ͼ��2�����ڣ�2���Ļ����ϣ�������P��A���������A��F��B��A�˶�һ��ֹͣ���ٶ�Ϊÿ��5���ף�ͬʱ��Q��C���������C��D��E��C�˶�һ��ֹͣ���ٶ�Ϊÿ��4���ף���P��Q�˶������У��ڼ���ʱ���ı���APCQ��ƽ���ı��Σ�
���𰸡�
��1��ƽ���ı��Σ�ƽ���ı��Σ�����
��2��
�⣺�������εı߳�AF=CF=xcm����BF=��8��x��cm��
��Rt��ABF��AB=4cm��
�ɹ��ɶ����ã�AB2+BF2=AF2��
��42+��8��x��2=x2��
��ã�x=5��
��AF=5
��3��
��������ã�P��AF��ʱ��Q��CD�ϣ���ʱA��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�
ͬ��P��AB��ʱ��Q��DE��CE�ϣ�Ҳ���ܹ���ƽ���ı��Σ�
��ֻ�е�P����BF�ϣ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��
PC=QA��
�ߵ�P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬
��PC=5t��QA=12��4t��
��5t=12��4t��
��ã�t= ![]() ��
��
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��t= ![]() �룮
�룮
���������⣺��1������EΪAD���е�ʱ���ı���AFCEΪƽ���ı��Σ��������£�
���ı���ABCD�Ǿ��Σ�
��AD��BC��OA=OC��
���CAD=��ACB����AEF=��CFE��
�ڡ�AOE�͡�COF�У� 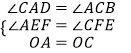 ��
��
���AOE�ա�COF��AAS����
��AE=CF��
�֡�AE��CF��
���ı���AFCEΪƽ���ı��Σ�
����EΪAD���е�ʱ��AE=CF��AE��CF��
���ı���AFCEΪƽ���ı��Σ�
��EF��ACʱ���ı���AFCEΪ���Σ��������£�
���ɢ�֪�ı���AFCEΪƽ���ı��Σ�
��EF��AC��
���ı���AFCEΪ���Σ�
���Դ��ǣ�ƽ���ı��Σ�ƽ���ı��Σ����Σ�
�����㾫����������Ĺؼ���������ɶ����ĸ�������֪ʶ������ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2���Լ���ƽ���ı��ε����ʵ����⣬�˽�ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�֣�