题目内容
如图,抛物线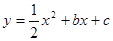 (b,c是常数,且c<0)与
(b,c是常数,且c<0)与 轴分别交于点A、B(点A位于点B的左侧),与
轴分别交于点A、B(点A位于点B的左侧),与 轴的负半轴交于点C,点A的坐标为(-1,0).
轴的负半轴交于点C,点A的坐标为(-1,0).

(1)请直接写出点OA的长度;
(2)若常数b,c满足关系式: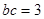 .求抛物线的解析式.
.求抛物线的解析式.
(3)在(2)的条件下,点P是 轴下方抛物线上的动点,连接PB、PC.设△PBC的面积为S.
轴下方抛物线上的动点,连接PB、PC.设△PBC的面积为S.
①求S的取值范围;
②若△PBC的面积S为整数,则这样的△PBC共有多少个(直接写出结果)?
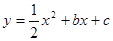 (b,c是常数,且c<0)与
(b,c是常数,且c<0)与 轴分别交于点A、B(点A位于点B的左侧),与
轴分别交于点A、B(点A位于点B的左侧),与 轴的负半轴交于点C,点A的坐标为(-1,0).
轴的负半轴交于点C,点A的坐标为(-1,0).
(1)请直接写出点OA的长度;
(2)若常数b,c满足关系式:
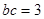 .求抛物线的解析式.
.求抛物线的解析式.(3)在(2)的条件下,点P是
 轴下方抛物线上的动点,连接PB、PC.设△PBC的面积为S.
轴下方抛物线上的动点,连接PB、PC.设△PBC的面积为S.①求S的取值范围;
②若△PBC的面积S为整数,则这样的△PBC共有多少个(直接写出结果)?
(1)OA=1;(2)抛物线的解析式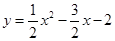 ;(3)①0<S<5;②
;(3)①0<S<5;② +c,﹣2c;11.
+c,﹣2c;11.
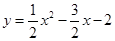 ;(3)①0<S<5;②
;(3)①0<S<5;② +c,﹣2c;11.
+c,﹣2c;11.试题分析:(1)由点A的坐标为(-1,0)可得:OA=1;
(2)根据抛物线
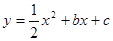 过点A (-1,0),得到:b = c+
过点A (-1,0),得到:b = c+ ,联立
,联立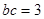 ,求出b,c的值即可;
,求出b,c的值即可;(3)①分两种情况进行讨论:(Ⅰ)当﹣1<x<0时;(Ⅱ)当0<x<4时;
②由0<S<5,S为整数,得出S=1,2,3,4.分两种情况进行讨论:(Ⅰ)当﹣1<x<0时,(Ⅱ)当0<x<4时.
试题解析:(1)OA=1;
(2)∵抛物线
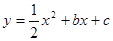 过点A (-1,0),
过点A (-1,0),∴b=c+
 ,
,∵
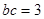 ,
,∴
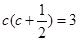 ,
,∵c<0,
∴
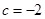 ,
,∴
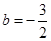 ,
,∴抛物线的解析式
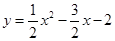 ;
;(3)①设点P坐标为(x,
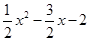 ).
).∵点A的坐标为(﹣1,0),点B坐标为(4,0),点C坐标为(0,﹣2),
∴AB=5,OC=2,直线BC的解析式为y=
 x﹣2.
x﹣2.分两种情况:
(Ⅰ)当﹣1<x<0时,0<S<S△ACB.
∵S△ACB=
 AB•OC=5,
AB•OC=5,∴0<S<5;
(Ⅱ)当0<x<4时,过点P作PG⊥x轴于点G,交CB于点F.
∴点F坐标为(x,
 x﹣2),
x﹣2),∴PF=PG﹣GF=﹣(
 x2﹣
x2﹣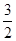 x﹣2)+(
x﹣2)+( x﹣2)=﹣
x﹣2)=﹣ x2+2x,
x2+2x,∴S=S△PFC+S△PFB=
 PF•OB=
PF•OB= (﹣
(﹣ x2+2x)×4=﹣x2+4x=﹣(x﹣2)2+4,
x2+2x)×4=﹣x2+4x=﹣(x﹣2)2+4,∴当x=2时,S最大值=4,
∴0<S≤4.
综上可知0<S<5;
②∵0<S<5,S为整数,
∴S=1,2,3,4.
分两种情况:
(Ⅰ)当﹣1<x<0时,设△PBC中BC边上的高为h.
∵点A的坐标为(﹣1,0),点B坐标为(4,0),点C坐标为(0,﹣2),
∴AC2=1+4=5,BC2=16+4=20,AB2=25,
∴AC2+BC2=AB2,∠ACB=90°,BC边上的高AC=
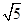 .
.∵S=
 BC•h,∴h=
BC•h,∴h=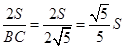 .
.如果S=1,那么h=
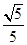 ×1=
×1=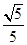 <
<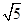 ,此时P点有1个,△PBC有1个;
,此时P点有1个,△PBC有1个;如果S=2,那么h=
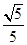 ×2=
×2=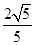 <
<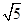 ,此时P点有1个,△PBC有1个;
,此时P点有1个,△PBC有1个;如果S=3,那么h=
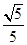 ×3=
×3=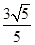 <
<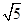 ,此时P点有1个,△PBC有1个;
,此时P点有1个,△PBC有1个;如果S=4,那么h=
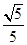 ×4=
×4=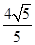 <
<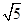 ,此时P点有1个,△PBC有1个;
,此时P点有1个,△PBC有1个;即当﹣1<x<0时,满足条件的△PBC共有4个;
(Ⅱ)当0<x<4时,S=﹣x2+4x.
如果S=1,那么﹣x2+4x=1,即x2﹣4x+1=0,
∵△=16﹣4=12>0,∴方程有两个不相等的实数根,此时P点有2个,△PBC有2个;
如果S=2,那么﹣x2+4x=2,即x2﹣4x+2=0,
∵△=16﹣8=8>0,∴方程有两个不相等的实数根,此时P点有2个,△PBC有2个;
如果S=3,那么﹣x2+4x=3,即x2﹣4x+3=0,
∵△=16﹣12=4>0,∴方程有两个不相等的实数根,此时P点有2个,△PBC有2个;
如果S=4,那么﹣x2+4x=4,即x2﹣4x+4=0,
∵△=16﹣16=0,∴方程有两个相等的实数根,此时P点有1个,△PBC有1个;
即当0<x<4时,满足条件的△PBC共有7个;
综上可知,满足条件的△PBC共有4+7=11个.
故答案为
 +c,﹣2c;11.
+c,﹣2c;11.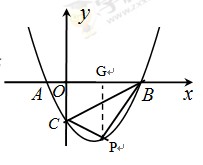 .
.
练习册系列答案
相关题目

 与坐标轴交于
与坐标轴交于 三点,点
三点,点 的横坐标为
的横坐标为 ,过点
,过点 的直线
的直线 与
与 轴交于点
轴交于点 ,点
,点 是线段
是线段 上的一个动点,
上的一个动点, 于点
于点 .若
.若 ,且
,且 .
.
 的值
的值 的坐标(其中
的坐标(其中 用含
用含 的式子表示):
的式子表示): 为等腰三角形?
为等腰三角形? 的对称轴是( )
的对称轴是( )



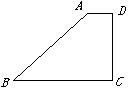
 中,
中,  , 高
, 高 (如图1). 动点
(如图1). 动点 同时从点
同时从点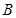 出发, 点
出发, 点 沿
沿 运动到点
运动到点 停止, 点
停止, 点 沿
沿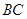 运动到点
运动到点 时,点
时,点 (s)时,
(s)时,  的面积为
的面积为 (如图2). 分别以
(如图2). 分别以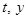 为横、纵坐标建立直角坐标系, 已知点
为横、纵坐标建立直角坐标系, 已知点 边上从
边上从 运动时,
运动时,  与
与 .
.

 的长度;
的长度; 边上和
边上和 边上运动时,
边上运动时,  (x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>﹣1时,y随x的增大而减小,其中正确结论的个数为( )
(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>﹣1时,y随x的增大而减小,其中正确结论的个数为( ) 或
或 .其中正确的是( )
.其中正确的是( )
 的顶点坐标是( )
的顶点坐标是( )