题目内容
【题目】如图,平面内的两条直线l1、l2,点A、B在直线l2上,过点A、B两点分别作直线l1的垂线,垂足分别为A1、B1,我们把线段A1B1叫做线段AB在直线l2上的正投影,其长度可记作T(AB,CD)或T(AB,l2),特别地,线段AC在直线l2上的正投影就是线段A1C,请依据上述定义解决如下问题.
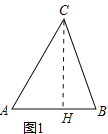
(1)如图1,在锐角△ABC中,AB=5,T(AC,AB)=3,则T(BC,AB)= ;
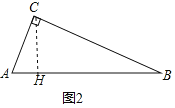
(2)如图2,在Rt△ABC中,∠ACB=90°,T(AC,AB)=4,T(BC,AB)=9,求△ABC的面积;
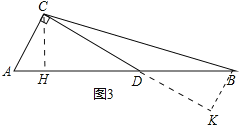
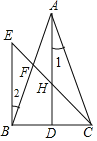
(3)如图3,在钝角△ABC中,∠A=60°,点D在AB边上,∠ACD=90°,T(AD,AC)=2,T(BC,AB)=6,求T(BC,CD).


【答案】(1)2 ;(2)△ABC的面积=39;(3)T(BC,CD)=![]()
【解析】
(1)如图1,过C作CH⊥AB,根据正投影的定义求出BH的长即可;
(2)如图2,过点C作CH⊥AB于H,由正投影的定义可知AH=4,BH=9,再根据相似三角形的性质求出CH的长即可解决问题;
(3)如图3,过C作CH⊥AB于H,过B作BK⊥CD于K,求出CD、DK即可得答案.
(1)如图1,过C作CH⊥AB,垂足为H,
∵T(AC,AB)=3,
∴AH=3,
∵AB=5,
∴BH=AB-AH=2,
∴T(BC,AB)=BH=2,
故答案为:2;
(2)如图2,过点C作CH⊥AB于H,
则∠AHC=∠CHB=90°,
∴∠B+∠HCB=90°,
∵∠ACB=90°,
∴∠B+∠A=90°
∴∠A=∠HCB,
∴△ACH∽△CBH,
∴CH:BH=AH:CH,
∴CH2=AH·BH,
∵T(AC,AB)=4,T(BC,AB)=9,
∴AH=4,BH=9,
∴AB=AH+BH=13,CH=6,
∴S△ABC=(AB·CH)÷2=13×6÷2=39;
(3)如图3,过C作CH⊥AB于H,过B作BK⊥CD于K,
∵∠ACD=90°,T(AD,AC)=2,
∴AC=2,
∵∠A=60°,
∴∠ADC=∠BDK=30°,
∴CD=AC·tan60°=2![]() ,AD=2AC=4,AH=
,AD=2AC=4,AH=![]() AC=1,
AC=1,
∴DH=4-1=3,
∵T(BC,AB)=6,CH⊥AB,
∴BH=6,
∴DB=BH-DH=3,
在Rt△BDK中,∠K=90°,BD=3,∠BDK=30°,
∴DK=BD·cos30°=![]() ,
,
∴T(BC,CD)=CK=CD+DK=![]() +
+![]() =
=![]() .
.