题目内容
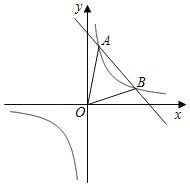
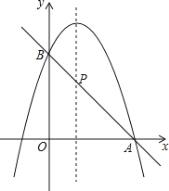
【题目】如图,二次函数y=﹣x2+2x+m的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P.
(1)求点B的坐标;
(2)求点P的坐标.
【答案】(1)B(0,3),(2)P(1,2)
【解析】
(1)把点A(3,0)代入二次函数的解析式求出m,即可确定二次函数的解析式,然后由解析式可得点B的坐标;
(2)根据A、B坐标求出直线AB的解析式,然后根据抛物线的对称轴可得P点横坐标,代入直线解析式可求得点P的坐标.
解:(1)∵二次函数的图象过点A(3,0),
∴0=9+6+m,
∴m=3,
∴二次函数的解析式为:y=x2+2x+3,
令x=0,得y=3,
∴B(0,3);
(2)设直线AB的解析式为:y=kx+b(k≠0),
∴![]() ,解得:
,解得:![]() ,
,
∴直线AB的解析式为:y=x+3,
∵抛物线y=x2+2x+3的对称轴为:x=1,
把x=1代入y=x+3得y=2,
∴P(1,2).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目