题目内容
【题目】△ABC和△CDE是以C为公共顶点的两个三角形.
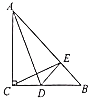
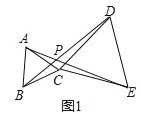
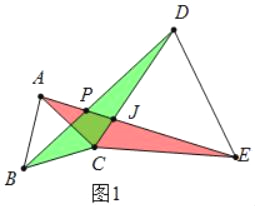
(1)如图1,当△ABC和△CDE都是等边三角形时,连接BD、AE相交于点P.求∠DPE的度数;
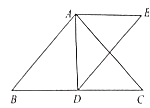
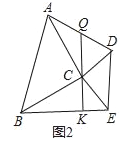
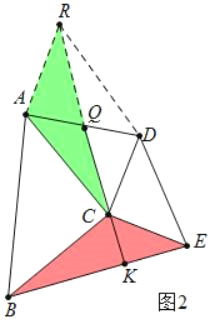
(2)如图2,当△ABC和△CDE都是等腰直角三角形,且∠ACB=∠DCE=90°时,连接AD、BE,Q为AD中点,连接QC并延长交BE于K.求证:QK⊥BE;
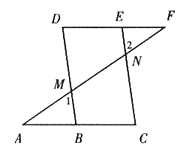
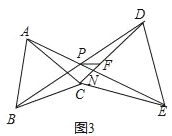
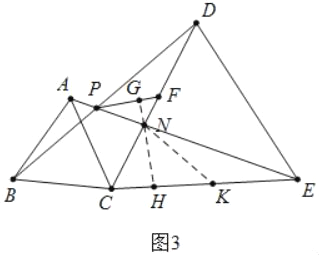
(3)在(1)的条件下,N是线段AE与CD的交点,PF是∠DPE的平分线,与DC交于点F,CN=2![]() ,∠PFN=45°,求FN的长.
,∠PFN=45°,求FN的长.
【答案】(1)60°;(2)见解析;(3)![]()
【解析】试题分析:(1)只要证明△BCD≌△ACE,可得∠BDC=∠AEC,利用“8字型”证明∠DPJ=∠JCE=60°即可;
·(2)如图2中,延长CQ到R,使得CQ=QR,连接AR、DR.只要证明△ACR≌△BCE,可得∠ACR=∠CBE,由∠ACR+∠BCK=90°,推出∠CBE+∠BCK=90°,,可得∠CKB=90°,即CK⊥BE.
(3)如图3中,作NH⊥EC于H,NG⊥PF于G,在EH上取一点K使得KN=KE.提供解直角三角形求出CE、DE、NE,再利用相似三角形的性质可得DE2=NE·PE,求出PE、PN,由此即可解决问题;
解:(1)如图1中,设AE交CD于J.
∵△ABC和△CDE都是等边三角形,
∴CB=CA,CD=CE,∠BCA=∠DCE,
∴BCD=∠ACE,
∴△BCD≌△ACE,
∴∠BDC=∠AEC,
∵∠PJD=∠CJE,
∴∠DPJ=∠JCE=60°,
∴∠DPE=60°.
(2)如图2中,延长CQ到R,使得CQ=QR,连接AR、DR.
∵△ABC和△CDE都是等腰直角三角形,
∴∠ACB=∠DCE=90°,AC=BC,CE=CD,
∴∠BCE+∠ACD=180°,
∵AQ=DQ,CQ=QR,
∴四边形ACDR是平行四边形,
∴AR=CD=CE,AR∥CD,
∴∠CAR+∠ACD=180°,
∴∠BCE=∠CAR,∵CA=CB,AR=CE,
∴△ACR≌△BCE,
∴∠ACR=∠CBE,
∵∠ACR+∠BCK=90°,
∴∠CBE+∠BCK=90°,
∴∠CKB=90°,即CK⊥BE.
(3)如图3中,作NH⊥EC于H,NG⊥PF于G,在EH上取一点K使得NK=EK.
∵∠DPE=60°,PF平分∠DPE,
∴∠NPPF=30°,
∵∠PFN=45°,∠NGF=90°,
∴GF=GN=![]() PN,FN=
PN,FN=![]() GN,
GN,
∴∠PNF=∠CNE=105°,∠CEN=15°,
∵KN=KE,
∴∠KNE=∠KEN=15°,
∴∠NKH=30°,
在Rt△CNH中,∵CN=2![]() ,∠CNH=30°,
,∠CNH=30°,
∴CH=![]() CN=
CN=![]() ,NH=
,NH=![]() CH=
CH=![]() ,
,
在Rt△NKH中,NK=KE=2NH=2![]() ,HK=
,HK=![]() NH=3
NH=3![]() ,
,
∴EN=![]() =
=![]() =6+2
=6+2![]() ,CE=DE=4
,CE=DE=4![]() +2
+2![]()
∵∠DEN=∠PED,∠EDN=∠EPD,
∴△DEN∽△PED,
∴DE2=NEPE,
∴可得PE=![]() ,PN=PE﹣EN=
,PN=PE﹣EN=![]() ,
,
∴FN=![]() ×
×![]() ×
×![]() =
=![]() .
.

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案【题目】![]() 开通了,中国联通公布了资费标准,其中包月
开通了,中国联通公布了资费标准,其中包月![]() 元时,超出部分国内拨打
元时,超出部分国内拨打![]() 元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
时间/分 | 1 | 2 | 3 | 4 | 5 | … |
电话费/元 | 0.36 | 0.72 | 1.08 | 1.44 | 1.80 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用![]() 表示超出时间,
表示超出时间,![]() 表示超出部分的电话费,那么
表示超出部分的电话费,那么![]() 与
与![]() 的关系式是什么?
的关系式是什么?
(3)如果打电话超出![]() 分钟,需多付多少电话费?
分钟,需多付多少电话费?
(4)某次打电话的费用超出部分是![]() 元,那么小明的爸爸打电话超出几分钟?
元,那么小明的爸爸打电话超出几分钟?