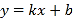Question

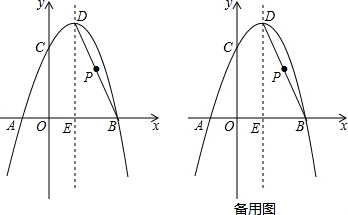
【题目】如图，△AOB是直角三角形，∠AOB=90°，OB=2OA，点A在反比例函数y= 的图象上．若点B在反比例函数y= 的图象上，则k的值为 ．

Answer 1

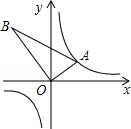
【答案】﹣4
【解析】解：过点A，B作AC⊥x轴，BD⊥x轴，分别于C，D．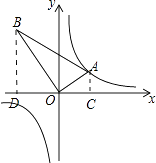
设点A的坐标是（m，n），则AC=n，OC=m．
∵∠AOB=90°，
∴∠AOC+∠BOD=90°．
∵∠DBO+∠BOD=90°，
∴∠DBO=∠AOC．
∵∠BDO=∠ACO=90°，
∴△BDO∽△OCA．
∴ ．
∵OB=2OA，
∴BD=2m，OD=2n．
因为点A在反比例函数y= 的图象上，
∴mn=1．
∵点B在反比例函数y= 的图象上，
∴B点的坐标是（﹣2n，2m）．
∴k=﹣2n2m=﹣4mn=﹣4．
故答案为：﹣4．
要求函数的解析式只要求出B点的坐标就可以，过点A，B作AC⊥x轴，BD⊥x轴，分别于C，D．根据条件得到△ACO∽△ODB，得到： =2，然后用待定系数法即可．