题目内容
【题目】设x是实数,y=|x-1|+|x+1|,下列结论正确的是( ).
A.y没有最小值
B.只有一个x使y取到最小值
C.有有限多个x(不止一个)使y取到最小值
D.有无穷多个x使y取到最小值
【答案】D
【解析】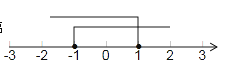 从数轴上可知,区间[-1,1]上的任一点x到点1与点-1的距离之和均为2;区间[-1,1]之外的点x 到点1与点-1的距离之和均大于2.
从数轴上可知,区间[-1,1]上的任一点x到点1与点-1的距离之和均为2;区间[-1,1]之外的点x 到点1与点-1的距离之和均大于2.
所以函数y=|x-1|+|x+1|当-1≤x≤1时,取得最小值2.
A.y在区间[-1,1]上取得最小值2;故本选项错误;
B.y在区间[-1,1]上的任一点x到点1与点-1的距离之和均为2;故本选项错误;
C.y在区间[-1,1]之外的点x 到点1与点-1的距离之和均大于2,且无限大,所以y在区间[-1,1]之外的点没有最大值;故本选项错误;
D.y在区间[-1,1]上的任一点x到点1与点-1的距离之和均为最小值2,所以有无穷多个x使y取到最小值.故本选项正确;选:D.
【考点精析】认真审题,首先需要了解一次函数的性质(一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小).

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目