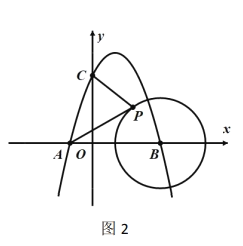题目内容
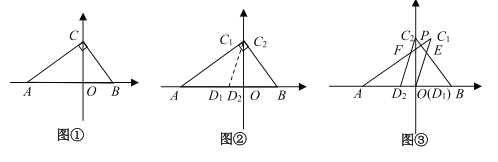
【题目】将一张直角三角形纸片![]() 放置在平面直角坐标系中,点A、B在x轴上,点C在y轴上,
放置在平面直角坐标系中,点A、B在x轴上,点C在y轴上,![]() ,且
,且![]() ,
,![]() .
.
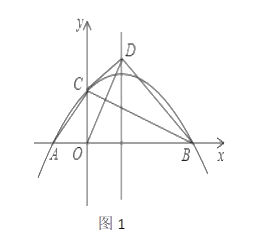
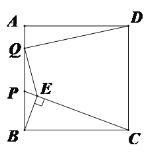
(Ⅰ)如图①,求点C的坐标;
(Ⅱ)如图②,沿斜边![]() 的中线
的中线![]() 把这张纸片剪成
把这张纸片剪成![]() 和
和![]() 两个三角形,将
两个三角形,将![]() 沿直线
沿直线![]() 方向平移(点A、
方向平移(点A、![]() 、
、![]() 、B始终在同一直线上),当点
、B始终在同一直线上),当点![]() 与点
与点![]() 重合时停止平移,
重合时停止平移,
①如图③,在平移的过程中,![]() 与
与![]() 交于点E,
交于点E,![]() 与
与![]() 、
、![]() 分别交于点F、P,当点
分别交于点F、P,当点![]() 平移到原点时,求
平移到原点时,求![]() 的长;
的长;
②在平移的过程中,当![]() 和
和![]() 重叠部分的面积最大时,求此时点
重叠部分的面积最大时,求此时点![]() 的坐标.(直接写出结论即可)
的坐标.(直接写出结论即可)
【答案】(I)点C的坐标为![]() ;(Ⅱ)①
;(Ⅱ)①![]() ,②
,②![]()
【解析】
(Ⅰ)利用勾股定理求出AB=10,再利用面积法求出OC即可得到答案;
(Ⅱ)①根据直角三角形斜边中线等于斜边一半及平行线的性质证得![]() ,利用勾股定理求出
,利用勾股定理求出![]() ,即可得到答案;
,即可得到答案;
②设平移的距离![]() 为x,
为x,![]() 和
和![]() 重叠部分面积为y,作
重叠部分面积为y,作![]() 的
的![]() 边上的高
边上的高![]() ,设
,设![]() 为h,根据
为h,根据![]() ,
,![]() 求出
求出![]() ,求出
,求出![]() ,根据二次函数的性质即可得到答案.
,根据二次函数的性质即可得到答案.
解:(I)在![]() 中,
中,![]()
∵![]() ,
,
即![]() ,
,
∴![]() .
.
∴点C的坐标为![]()
(Ⅱ)①∵![]() ,
,
![]() ,
,
又∵![]() ,
,![]() 是斜边
是斜边![]() 上的中线,
上的中线,
∴![]() ,即
,即![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]()
在![]() 中,
中, .
.
∴![]() .
.
②![]()
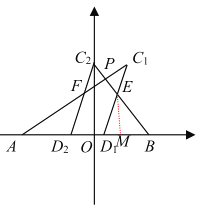
如图,设平移的距离![]() 为x,
为x,
![]() 和
和![]() 重叠部分面积为y,由题意得,
重叠部分面积为y,由题意得,
![]() ,
,![]() ,
,
又因为![]() ,
,
∴![]() .
.
∴![]() .
.
作![]() 的
的![]() 边上的高
边上的高![]() ,设
,设![]() 为h,
为h,
由平移可知![]() .
.
在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
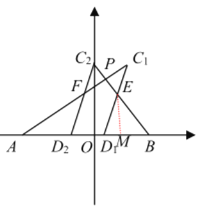
∴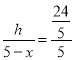 .
.
∴![]() ,
,![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
∴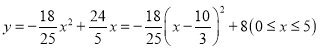 .
.
∴当![]() 时,y有最大值8.
时,y有最大值8.
此时![]() .
.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案【题目】茶叶是安徽省主要经济作物之一,2020年新茶上市期间,某茶厂为获得最大利益,根据市场行情,把新茶价格定为400元/kg,并根据历年的相关数据整理出第x天(1≤x≤15,且x为整数)制茶成本(含采摘和加工)和制茶量的相关信息如下表.假定该茶厂每天制作和销售的新茶没有损失,且能在当天全部售出(当天收入=日销售额-日制茶成本)
制茶成本(元/kg) | 150+10x |
制茶量(kg) | 40+4x |
(1)求出该茶厂第10天的收入;
(2)设该茶厂第x天的收入为y(元).试求出y与x之间的函数关系式,并求出y的最大值及此时x的值.