题目内容
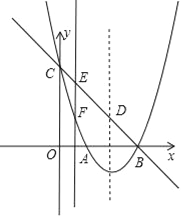
【题目】如图①是一个直角三角形纸片,∠C=90°,AB=13cm,BC=5cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD(如图②),求DC的长.

【答案】DC的长为![]()
【解析】
利用勾股定理列式求出AC,根据翻折变换的性质可得BC′=BC,DC′=DC,设DC=x,表示出AD,然后利用勾股定理列方程求解即可.
∵∠C=Rt∠,AB=13cm,BC=5cm,
∴AC=![]() =12cm,
=12cm,
∵折叠点C落在斜边上的点C′处,
∴BC′=BC=5,DC′=DC,
∴AC′=AB﹣BC′=13﹣5=8cm,
设DC=x,则AD=AC﹣DC=12﹣x,
DC′=x,
在Rt△AC′D中,根据勾股定理得,AC′2+DC′2=AD2,
即82+x2=(12﹣x)2,
∴x=![]() ,
,
∴DC的长为![]() .
.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
【题目】永辉超市进行有奖促销活动.活动规则:购买500元商品就可以获得一次转转盘的机会(转盘分为5个扇形区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以获得该区域相应等级奖品一件.商场工作人员在制作转盘时,将获奖扇形区域圆心角分配如下表:
奖次 | 特等奖 | 一等奖 | 二等奖 | 三等奖 |
圆心角 |
|
|
|
|
促销公告
凡购买我商场商品均有可能获得下列大奖:
特等奖:彩电一台 一等奖:自行车一辆 二等奖:圆珠笔一支 三等奖:卡通画一张
(1)获得圆珠笔的概率是多少?
(2)不获奖的概率是多少?
(3)如果不用转盘,请设计一种等效试验方案.(要求写清楚替代工具和实验规则)