题目内容
【题目】如图，四边形ABCD中，AB＝AD，点B关于AC的对称点B′ 恰好落在CD上，若∠BAD＝110°，则∠ACB的度数为( )
A.40°B.35°C.60°D.70°
【答案】B
【解析】
连接AB'，BB'，过A作AE⊥CD于E，依据∠BAC=∠B'AC，∠DAE=∠B'AE，即可得出∠CAE=
∠BAD，再根据四边形内角和以及三角形外角性质，即可得到∠ACB=∠ACB'=90°-∠BAD．
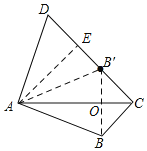
解：如图，连接AB'，BB'，过A作AE⊥CD于E，
∵点B关于AC的对称点B'恰好落在CD上，
∴AC垂直平分BB'，
∴AB=AB'，
∴∠BAC=∠B'AC，
∵AB=AD，
∴AD=AB'，
又∵AE⊥CD，
∴∠DAE=∠B'AE，
∴∠CAE=∠BAD=55°，
又∵∠AEC=90°，
∴∠ACB=∠ACB'=35°，
故选：B．
练习册系列答案
名校课堂系列答案
相关题目
【题目】如图1，点O是矩形ABCD的中心（对角线的交点），AB=4cm，AD=6cm．点M是边AB上的一动点，过点O作ON⊥OM，交BC于点N，设AM=x，ON=y，今天我们将根据学习函数的经验，研究函数值y随自变量x的变化而变化的规律．
下面是某同学做的一部分研究结果，请你一起参与解答：
（1）自变量x的取值范围是______；
（2）通过计算，得到了x与y的几组值，如下表：
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 2.40 | 2.24 | 2.11 | 2.03 | __ | __ | 2.11 | 2.24 | 2.40 |
请你补全表格（说明：补全表格时相关数值保留两位小数，参考数据：
≈3.04，
≈6.09）
（3）在如图2所示的平面直角坐标系中，画出该函数的大致图象．
（4）根据图象，请写出该函数的一条性质．
