Question

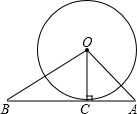
已知：如图，圆心A(0，-3)，⊙A与x轴相切，⊙B的圆心B在x轴的正半轴上，且⊙A与⊙B外切于P点，两圆的内公切线MP交y轴于M，交x轴于N．

(1)求证：△AOB∽△NPB；

(2)设⊙A半径为r₁，⊙B半径为r₂，若r₁∶r2=3∶2，求点M、N的坐标及公切线MP的函数解析式；

(3)设点B(x₁，0)，点B关于y轴的对称点是B′(x₂，0)，若x₁·x₂=-6，求过B′、A、B三点的抛物线的解析式；

(4)若⊙A的位置大小不变，圆心B在x正半轴上移动，并始终有⊙B与⊙A外切，过点M作⊙B的切线MC，C为切点，MC=3时，B点在x轴的什么位置？从你的解答中能获得什么猜想？

 

Answer 1

答案：
解析：

(1)∵　MP为⊙O的公切线， ∴　∠NPB=∠AOB=90°，又∠NBP=∠ABO， ∴　△AOB∽△NPB．　　　　　　　　　　　　　　　　　　　　　　　　　　3分 (2)M(0，2)，N(，0)，y=；　　　　　　　　　　　　　　　　　　　6分 (3)y=x2-3；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 9分 (4)当MC=时，点B的坐标为(，0)，四边形MOBC为矩形，点B的横坐标为(，0)与点C的横坐标相同．　　12分