题目内容
【题目】已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的周长取最小值时,∠APB的度数为°.
【答案】100
【解析】如图,作出P点关于OM、ON的对称点P1 , P2连接P1 , P2交OM,ON于A、B两点,此时△PAB的周长最小,由题意可知∠P1PP2=180°-∠MON=180°-40°=140°,
∴∠P1PA+∠P2PB=∠P1+∠P2=180°-∠P1PP2=40°,
∴∠APB=140°-40°=100°.
故答案为:100°.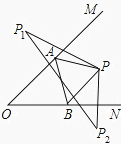
作出P点关于OM、ON的对称点P1 , P2连接P1 , P2交OM,ON于A、B两点,此时△PAB的周长最小,再由四边形内和定理即可求出答案.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目