��Ŀ����
����Ŀ���ۺ���̽����
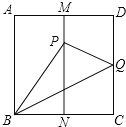
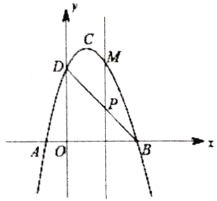
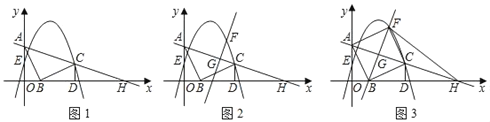
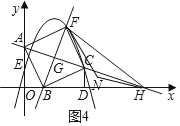
��ͼ1��Rt��AOB��ֱ�Ƕ���O������ԭ�㣬��A��y���������ϣ���B��x���������ϣ�OA��4��OB��2�����߶�AB�Ƶ�B˳ʱ����ת90��õ��߶�BC������C��CD��x���ڵ�D��������y��ax2+3x+c������C����y�ύ�ڵ�E(0��2)��ֱ��AC��x�ύ�ڵ�H��
(1)���C�����꼰�����ߵı���ʽ��
(2)��ͼ2����֪��G���߶�AH�ϵ�һ�����㣬����G��AH�Ĵ��߽��������ڵ�F(��F�ڵ�һ����)�����G�ĺ�����Ϊm��
����G���������ú�m�Ĵ���ʽ��ʾΪ�� ����
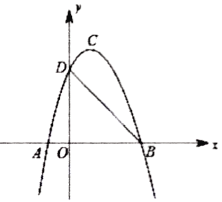
����ͼ3����ֱ��FG������Bʱ�����F�����꣬�ж��ı���ABCF����״��֤�����ۣ�
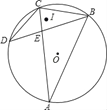
��������ǰ���£�����FH����N������ƽ���ڵĵ㣬����F��H��NΪ��������������FHCȫ�ȣ���ֱ��д����N�����꣮
���𰸡�(1)C(6��2)�������߽���ʽΪy����![]() x2+3x+2��(2)�٩�
x2+3x+2��(2)�٩�![]() m+4�����ı���ABCF�������Σ����ɼ��������۵�N����Ϊ(
m+4�����ı���ABCF�������Σ����ɼ��������۵�N����Ϊ(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��(10��4)��
)��(10��4)��
��������
��1�����߶�AB��ת90���BC��CD��x���֤�á�BDC�ա�AOB������BD=OA=4��CD=OB=2����õ�C���꣬�����ɵ�E��C�����ô���ϵ���������������߽���ʽ��
��2�����ɵ�A��C�����ô���ϵ������ֱ��AC����ʽ���ѵ�G������m���뼴�õ���m��ʾ��G�����꣮
����AB=BC��BG��AC�ɵ�AG=CG������GΪAC�е㣬�����е����깫ʽ�����G���꣬������ֱ��BG����ʽ������ֱ��BG�������߽���ʽ�ⷽ���鼴��õ�F���꣮����F��PF��y���ڵ�P���ӳ�DC��PF�ڵ�Q�����ݹ��ɶ������AB=BC=CF=AF=2![]() ���ж��ı���ABCF�����Σ����ɡ�ABC=90�㼴֤������ABCFΪ�����Σ�
���ж��ı���ABCF�����Σ����ɡ�ABC=90�㼴֤������ABCFΪ�����Σ�
����ֱ��AC����ʽ������x�ύ��H�����꣬���������빫ʽ��CF��CH�ij������N����Ϊ��s��t������s��t��ʽ�ӱ�ʾFN2��NH2���������ۣ�����FHC�ա�FHN����FN=FC��NH=CH���еù���s��t�ķ����飬��⼴�õ���N���ꣻ����FHC�ա�HFN����FN=CH��NH=FC��ͬ������õ�N���꣮
�⣺(1)��OA��4��OB��2��
��A(0��4)��B(2��0)��
���߶�AB�Ƶ�B˳ʱ����ת90���õ��߶�BC��
��AB��BC����ABC��90����
���ABO+��DBC����ABO+��OAB��90����
���DBC����OAB��
��CD��x���ڵ�D��
���BDC����AOB��90����
����BDC����AOB��
 ��
��
���BDC�ա�AOB(AAS)��
��BD��OA��4��CD��OB��2��
��OD��OB+BD��6��
��C(6��2)��
��������y��ax2+3x+c������C����E(0��2)��
�� ![]() ��ã�
��ã�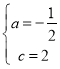 ��
��
�������߽���ʽΪy����![]() x2+3x+2.
x2+3x+2.
(2)�١�A(0��4)��
����ֱ��AC����ʽΪy��kx+4��
�ѵ�C����ã�6k+4��2����ã�k����![]() ��
��
��ֱ��AC��y����![]() x+4��
x+4��
����G��ֱ��AC�ϣ�������Ϊm��
��yG����![]() m+4��
m+4��
�ʴ�Ϊ����![]() m+4��
m+4��
�ڡ�AB��BC��BG��AC��
��AG��CG����GΪAC�е㣬
��G(3��3)��
��ֱ��BG����ʽΪy��gx+b��
�� ![]() ����ã�
����ã�![]() ��
��
��ֱ��BG��y��3x��6��
��ֱ��BG�������߽���ΪF���ҵ�F�ڵ�һ���ޣ�
�� 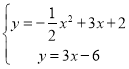 ��ã�
��ã� 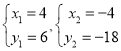 (��ȥ)��
(��ȥ)��
��F(4��6)��
�ж��ı���ABCF�������Σ��������£�
��ͼ1������F��FP��y���ڵ�P��PF�ӳ�����DC�ӳ��߽��ڵ�Q��
 ��
��
��PF��4��OP��DQ��6��PQ��OD��6��
��AP��OP��OA��6��4��2��FQ��PQ��PF��6��4��2��CQ��DQ��CD��6��2��4��
��AF��![]() ��FC��
��FC��![]() ��
��
��BC��AB��![]() ��
��
��AB��BC��CF��AF��
���ı���ABCF�����Σ�
�ߡ�ABC��90����
������ABCF��������.
�ۡ�ֱ��AC��y����![]() x+4��x�ύ�ڵ�H��
x+4��x�ύ�ڵ�H��
����![]() x+4��0����ã�x��12��
x+4��0����ã�x��12��
��H(12��0)��
��FC2��(6��4)2+(2��6)2��20��CH2��(12��6)2+(0��2)2��40��
���N����Ϊ(s��t)��
��FN2��(s��4)2+(t��6)2��NH2��(s��12)2+(t��0)2��
��ͼ2������FHC�ա�FHN����FN��FC��NH��CH��
 ��
��
�� ��ã�
��ã�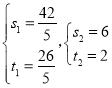 (����C)��
(����C)��
��N![]() ��
��
��ͼ3��4������FHC�ա�HFN����FN��CH��NH��FC��

�� ����ã�
����ã� ��
��
��N![]() ��
��
������������F��H��NΪ���������������FHCȫ��ʱ����N����Ϊ(![]() ��
��![]() )��
)��![]() ��
��