题目内容
【题目】在每个小正方形的边长为1的网格中，等腰直角三角形ACB与ECD的顶点都在网格点上，点N、M分别为线段AB、DE上的动点，且BN=EM． （Ⅰ）如图①，当BN= 
时，计算CN+CM的值等于 
（Ⅱ）当CN+CM取得最小值时，请在如图②所示的网格中，用无刻度的直尺，画出线段CN和CM，并简要说明点M和点N的位置是如何找到的（不要求证明）．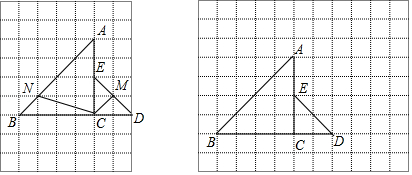
【答案】（1）当BN=EM= 
时，点N和点M在格点上， ∴CN+CM= 
+ 
= 
+ ；
⑵如图所示，取格点P、Q，使得PB=CE，PB⊥BC，QE=CB，QE⊥AC，
连接CP交AB于N，连接CQ交DE于M，则线段CN和CM即为所求．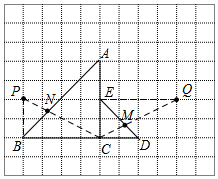
理由如下：根据等腰直角三角形ACB与ECD的顶点都在网格点上，可得∠PBN=∠CEM=45°，∠CBN=∠QEM=45°，而BN=EM，
故△BPN≌△ECM，△CBN≌△QEM，
∴PN=CM，CN=QM，
∴当P，N，C三点共线时，CM+CN=PN+CN=PC（最短），
当Q，M，C三点共线时，CM+CN=CM+MQ=QC（最短），
∴点M和点N的位置符合题意
【解析】（1）根据当BN=EM= 
时，点N和点M在格点上，运用勾股定理进行计算即可得到CN+CM的值；（2）取格点P、Q，使得PB=CE，PB⊥BC，QE=CB，QE⊥AC，连接CP交AB于N，连接CQ交DE于M，则根据全等三角形的对应边相等，以及两点之间线段最短，可得线段CN和CM即为所求．
【考点精析】本题主要考查了勾股定理的概念的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．
练习册系列答案
相关题目
