Question

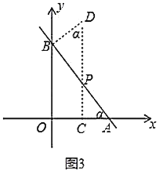
【题目】如图，已知直线分别交轴、轴于点、，抛物线过，两点，点是线段上一动点，过点作轴于点，交抛物线于点．

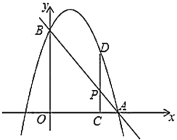
（1）若抛物线的解析式为，设其顶点为，其对称轴交于点．

①求点和点的坐标；

②在抛物线的对称轴上找一点，使的值最大，请直接写出点的坐标；

③是否存在点，使四边形为菱形？并说明理由；

（2）当点的横坐标为1时，是否存在这样的抛物线，使得以、、为顶点的三角形与相似？若存在，求出满足条件的抛物线的解析式；若不存在，请说明理由．

Answer 1

【答案】（1）①，②，③不存在，理由见解析；（2）存在，或．

【解析】

(1)①函数的对称轴为: ，故点，即可求解；

②设抛物与x轴左侧的交点为R(-1，0)，则点A与R关于抛物线的对称轴对称，连接RB并延长交抛物线的对称轴于点Q，则点Q为所求，即可求解

③四边形MNPD为菱形，首先PD＝MN，即，解得：或（舍去），故点，而，即可求解；

(2)分∠DBP为直角、∠BDP为直角两种情況，分别求解即可.

解：（1）①函数的对称轴为：，故点，

当时，，故点；

②设抛物线与轴左侧的交点为，则点与关于抛物线的对称轴对称，

连接并延长交抛物线的对称轴于点，则点为所求，

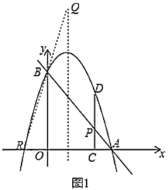
将、的坐标代入一次函数表达式：并解得：

直线的表达式为：，当时，，故点；

③不存在，理由：

设点，则点，

，

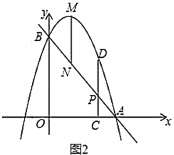
四边形为菱形，首先，

即，解得：或（舍去），

故点，而，

故不存在点，使四边形为菱形；

（2）当点的横坐标为1时，则其坐标为：，此时点、的坐标分别为：、

，

①当为直角时，以、、为顶点的三角形与相似，

则，，则，

，，

则，故点；

②当为直角时，以、、为顶点的三角形与相似，

则轴，则点、关于抛物线的对称轴对称，故点，

综上，点的坐标为：或，

将点、、的坐标代入抛物线表达式：并解得：

或．