题目内容
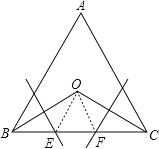
【题目】如图,在等边三角形ABC中,∠B、∠C的平分线相交于点O,作BO、CO的垂直平分线分别交BC于点E、F.小明说:“E、F是BC的三等分点.”你同意他的说法吗?请说明理由.

【答案】同意,理由见解析
【解析】试题分析:连接OE、OF,根据等边三角形角平分线的性质,可得∠OBC=∠OCB=30°,由BC的垂直平分线,可知BE=OE,∠EBO=∠EOB=30°,∠OEF=60°,再证,∠OFE=60°,得出△OEF为等边三角形,从而可知EF=OE=BE=OF=FC,得出结论.
试题解析:同意.理由如下:
连接OE、OF,
∵E为BO垂直平分线上的点,且∠OBC=30°,
∴BE=OE,∠EBO=∠EOB=30°,
∴∠OEF=∠EBO+∠EOB=60°,
同理,∠OFE=∠FCO+∠FOC=60°,
∴△OEF为等边三角形,
即EF=OE=BE,EF=OF=FC,
故E、F为BC的三等分点,
故该说法正确.

练习册系列答案
相关题目