题目内容
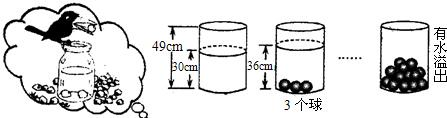
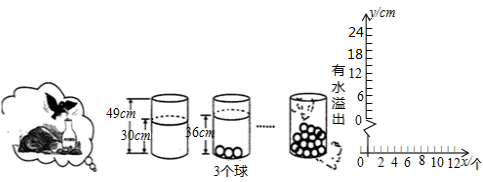
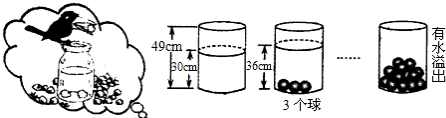
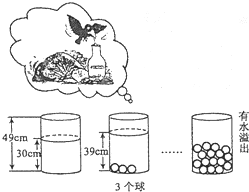 小明受《乌鸦喝水》故事的启发,利用量桶和体积相同的小球进行了如下图的操作,请根据图中所给信息,解答下列问题:
小明受《乌鸦喝水》故事的启发,利用量桶和体积相同的小球进行了如下图的操作,请根据图中所给信息,解答下列问题:(1)放入一个小球,量桶中水面升高
3
3
cm.(2)求放入球后量桶中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式(不要求写出自变量的取值范围).
(3)量桶中至少放入几个小球时有水溢出?
分析:(1)设每放入一个小球,量筒中的水面上升acm,根据条件建立方程求出其解即可;
(2)设放入球后量桶中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式为y=kx+b,由待定系数法就可求出结论;
(3)当y>49时,建立不等式求出其解即可.
(2)设放入球后量桶中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式为y=kx+b,由待定系数法就可求出结论;
(3)当y>49时,建立不等式求出其解即可.
解答:解:(1)每放入一个小球,量筒中的水面上升acm,由图象,得
30+3a=39,
解得:x=3,
故答案为:3;
(2)设放入球后量桶中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式为y=kx+b,由题意,得
,
解得:
.
∴函数关系式为:y=3x+30;
(3)由题意,得
3x+30>49,
解得:x>
,
∵x为整数,
∴x最小为7,
∴量桶中至少放入7个小球时有水溢出.
30+3a=39,
解得:x=3,
故答案为:3;
(2)设放入球后量桶中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式为y=kx+b,由题意,得
|
解得:
|
∴函数关系式为:y=3x+30;
(3)由题意,得
3x+30>49,
解得:x>
| 19 |
| 3 |
∵x为整数,
∴x最小为7,
∴量桶中至少放入7个小球时有水溢出.
点评:本题考查了列一元一次方程解实际问题的运用,待定系数法求函数的解析式的运用,列不等式解实际问题的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目