题目内容
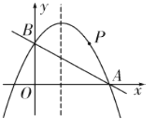
【题目】在平面直角坐标系xOy中,抛物线![]() 与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
(1)当![]() 时,
时,
①写出抛物线的对称轴;
②求抛物线的表达式;
(2)存在垂直于x轴的直线分别与直线![]() :
:![]() 和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)①由二次函数的对称轴方程可得出答案;
②根据题意求出B点坐标为(2,0),代入抛物线解析式![]() 可得出答案;
可得出答案;
(2)求出E(-![]() ,0),点D的坐标为(-
,0),点D的坐标为(-![]() ,0).①当b>0时,得出点A的坐标为(-2b,0),点B的坐标为(b,0),则-2b<-
,0).①当b>0时,得出点A的坐标为(-2b,0),点B的坐标为(b,0),则-2b<-![]() ,解不等式即可;②当b<0时,点A的坐标为(0,0),点B的坐标为(-b,0),则0<-
,解不等式即可;②当b<0时,点A的坐标为(0,0),点B的坐标为(-b,0),则0<-![]() ,解出b<-2.
,解出b<-2.
解:(1)当![]() 时,
时,![]() 化为
化为![]() .
.
①![]() .
.
②∵抛物线的对称轴为直线![]() ,
,
∴点D的坐标为(-1,![]() ),OD=1.
),OD=1.
∵OB=2OD,
∴ OB=2.
∵点A,点B关于直线![]() 对称,
对称,
∴点B在点D的右侧.
∴ 点B的坐标为(![]() ,
,![]() ).
).
∵抛物线![]() 与x轴交于点B(
与x轴交于点B(![]() ,
,![]() ),
),
∴ ![]() .
.
解得![]() .
.
∴抛物线的表达式为![]() .
.
(2)设直线![]() 与x轴交点为点E,
与x轴交点为点E,
当y=0时,![]()
∴ ![]()
∴ E(![]() ,0).
,0).
抛物线的对称轴为![]() ,
,
∴点D的坐标为(![]() ,
,![]() ).
).
①当![]() 时,
时,![]() .
.
∵OB=2OD,
∴ OB=b.
∴ 点A的坐标为(![]() ,
,![]() ),点B的坐标为(b,
),点B的坐标为(b,![]() ).
).
当![]() <
<![]() 时,存在垂直于x轴的直线分别与直线
时,存在垂直于x轴的直线分别与直线![]() :
:![]() 和抛物线交于点P,Q,且点P,Q均在x轴下方,
和抛物线交于点P,Q,且点P,Q均在x轴下方,

解得![]() .
.
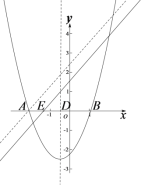
②当![]() 时,
时,![]() .
.
∴ ![]() .
.
∵OB=2OD,
∴ OB=-b.
∵抛物线![]() 与x轴交于点A,B,且A在B的左侧,
与x轴交于点A,B,且A在B的左侧,
∴ 点A的坐标为(![]() ,
,![]() ),点B的坐标为(-b,
),点B的坐标为(-b,![]() ).
).
当0<![]() 时,存在垂直于x轴的直线分别与直线
时,存在垂直于x轴的直线分别与直线![]() :
:![]() 和抛物线交于点P,Q,且点P,Q均在x轴下方,
和抛物线交于点P,Q,且点P,Q均在x轴下方,
解得b<-2.
综上,b的取值范围是![]() 或
或![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目