题目内容
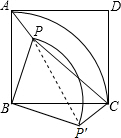
如图,已知点P是边长为5的正方形ABCD内的一点,连结PA,PB,PC,若PA=2,PB=4,∠APB=135°.
(1)将△PAB绕点B顺时针旋转90°,画出△P′CB的位置.
(2)①求PC的长;
②求△PAB旋转到△P′CB的过程中边PA所扫过区域的面积.

(1)将△PAB绕点B顺时针旋转90°,画出△P′CB的位置.
(2)①求PC的长;
②求△PAB旋转到△P′CB的过程中边PA所扫过区域的面积.

(1)如图所示:△P′CB即为所求;
(2)①连接PP′,
∵将△PAB绕点B顺时针旋转90°,
∴PB=P′B=4,A,P,P′在一条直线上,∠PP′C=∠BP'C-∠BP'P=135°-45°=90°,
∵∠APB=135°,
∴∠BPP′=45°,
∴△PBP′是等腰直角三角形,
∴PP′=4
,
∵P′C=PC=2,
∴PC=
=6;
②△PAB旋转到△P′CB的过程中边PA所扫过区域的面积为:
S扇形ABC+S△BCP′-S扇形PBP′-S△ABP=S扇形ABC-S扇形PBP′=
=
π.
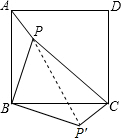
(2)①连接PP′,
∵将△PAB绕点B顺时针旋转90°,
∴PB=P′B=4,A,P,P′在一条直线上,∠PP′C=∠BP'C-∠BP'P=135°-45°=90°,
∵∠APB=135°,
∴∠BPP′=45°,
∴△PBP′是等腰直角三角形,
∴PP′=4
| 2 |

∵P′C=PC=2,
∴PC=
(4
|
②△PAB旋转到△P′CB的过程中边PA所扫过区域的面积为:
S扇形ABC+S△BCP′-S扇形PBP′-S△ABP=S扇形ABC-S扇形PBP′=
| 90π(52-42) |
| 360 |
| 9 |
| 4 |


练习册系列答案
相关题目