题目内容
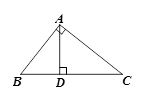
如图,△ABC中,∠BAC=90°,AD⊥BC于D,若AB=2,BC=3,则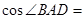 .
. 
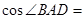 .
. 
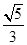
由AD⊥BC得到∠ADB=90°,根据等角的余角相等得到∠C=∠BAD,在△ABC中,利用勾股定理可计算出AC,然后根据余弦的定义得到cosC,即可得到cos∠BAD.
解答:解:∵AD⊥BC,
∴∠ADB=90°,
∴∠C=∠BAD,
在△ABC中,∠BAC=90°,AB=2,BC=3,
∴AC=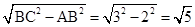 ,
,
∴cosC=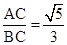 ,
,
∴cos∠BAD=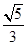 .
.
故答案为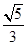 .
.
解答:解:∵AD⊥BC,
∴∠ADB=90°,
∴∠C=∠BAD,
在△ABC中,∠BAC=90°,AB=2,BC=3,
∴AC=
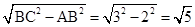 ,
,∴cosC=
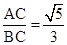 ,
,∴cos∠BAD=
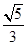 .
.故答案为
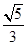 .
.
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 中,斜边
中,斜边 的长为
的长为 ,
, ,则直角边
,则直角边 的长是( )
的长是( )




 中,
中, ,则
,则
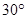 ,B村的俯角为
,B村的俯角为 .(如图).求A、B两个村庄间的距离.(结果精确到米,参考数据
.(如图).求A、B两个村庄间的距离.(结果精确到米,参考数据 )
)
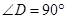 ,
,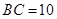 ,
,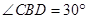 ,
,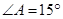 .
. 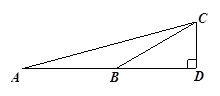
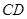 的长;
的长;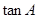 的值.
的值.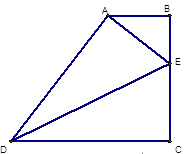

 是
是 的一个内角,抛物线
的一个内角,抛物线 的顶点在
的顶点在 轴上.
轴上. 求:AB边的长.
求:AB边的长.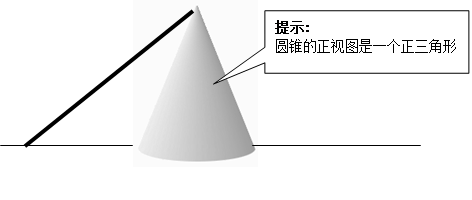
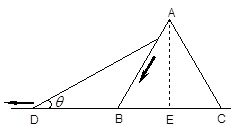
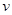 (木棒下滑为匀速)已知木棒与水平地面的夹角为
(木棒下滑为匀速)已知木棒与水平地面的夹角为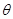 ,
,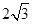
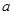 。问:当木棒顶端从A滑到B这个过程中,木棒末端的速度
。问:当木棒顶端从A滑到B这个过程中,木棒末端的速度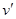 为多少?
为多少?